主讲：方敏文

一周强化

一、一周知识概述

(一)等腰三角形

　　1、有两条边相等的三角形叫做等腰三角形。如图所示，在△ABC中，若AB=AC，则△ABC是等腰三角形。

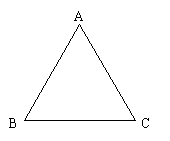
　　2、在等腰三角形中，相等的两边分别叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。如图所示，AB，AC叫做腰，BC叫做底边。∠A叫做顶角，∠B和∠C叫做底角。

　　3、顶角是直角的等腰三角形叫做等腰直角三角形。

（二）等腰三角形的性质

　　性质1：等腰三角形的两个底角相等（简写为“等边对等角”）。

　　性质2：等腰三角形顶角的角平分线、底边上的中线、底边上的高重合（简称“三线合一”）。

　　[说明]　等腰三角形是轴对称图形，有一条对称轴。

（三）等边三角形及其性质

　　1、三边都相等的三角形是等边三角形。

　　2、等边三角形的各角都相等，并且每一个角都等于60°。

　　3、等边三角形是轴对称图形，共有三条对称轴。

（四）等腰三角形的判定

　　如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写为“等角对等边”）。

　　[注意]　“等角对等边”，强调的是在同一个三角形中，否则不成立，这一点我们应特别注意。

（五）等边三角形的判定

　　1、三个角都相等的三角形是等边三角形。

　　2、有一个角是60°的等腰三角形是等边三角形。

（六)含有一个30°角的直角三角形的性质

　　在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

二、重难点知识归纳

　　（1）性质1提示由三角形的边的关系推出角的关系，同时也提供了证明两个角相等的一种新的方法．

　　（2）等腰三角形顶角的平分线、底边的中线、底边上的高互相重合是一个非常重要的性质，在今后的应用是非常广泛的．

　　（3）在叙述等腰三角形的判定定理时，要注意说成“如果一个三角形有两个底角相等，那么它的两腰相等”是错误的，因为在没有判定出它是等腰三角形以前，不能用“底角”“腰”等名词，只有等腰三角形才有“底角”、“腰”．

　　（4）几何作图必须熟练地运用各种图形的一些性质．

三、典型例题剖析

例1、如果等腰三角形的两边长分别为3和5，求这个三角形的周长。

分析：

　　欲求三角形的周长，即是求这个三角形的第三边，又因为这个三角形是等腰三角形，所以第三边一定与已知两边中的一边相等，至于是已知两边中的哪一条，则需由三角形三边关系来确定。

解：

　　若三角形的腰长为3，底边长为5时，则这个三角形的另一腰长是3，此时，3＋3>5，满足三角形的三边关系，则这个三角形的周长是：3＋3＋5=11。

　　若三角形的腰长为5，底边长为3时，则这个三角形的另一腰长是5，此时，3＋5>5，满足三角形的三边关系，则这个三角形的周长是：5＋5＋3=13。

　　∴这个三角形的周长为11或13。

例2、如图所示，已知长方形ABCD，把△ABC沿对角线AC折叠，交AD于点F，问△AFC是一个等腰三角形吗？为什么？

分析：

　　利用等腰三角形的判定来说明。

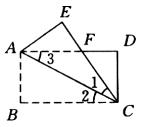
解：

　　△AFC是一个等腰三角形，理由如下：

　　∵△ACE是由△ABC折叠而成的，∴∠1=∠2。

　　又∵四边形ABCDE是长方形，∴AD∥BC。

　　∴∠2=∠3，∴∠1=∠3，∴FA=FC（等角对等边），

　　∴△AFC是等腰三角形。

例3、如图，点D在AC上，点E在AB上，且AB=AC，BC=BD，AD=DE=BE．求∠A的度数．

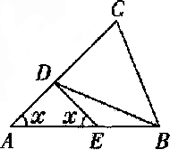
分析：

　　本题中没有给出一个角的度数，而要求∠A的度数，必然是运用三角形内角和定理，其解题思路是设某一个角的度数为x，其他各角都能用x的代数式表示，列出代数方程求解．

解：设∠A=x．

　　∵AD=DE=EB

　　∴∠DEA=∠A=x，∠EBD=∠EDB．

　　又∵∠DEA=∠EBD＋∠EDB，

　　∴∠EBD=∠EDB=．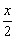

　　∴∠BDC=∠A＋∠ABD=．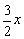

　　∵BD=BC，AB=AC，

　　∴∠BDC=∠BCD=∠ABC=．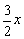

　　在△ABC中，∠A＋∠ABC＋∠ACB=180°，

　　即，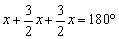

　　∴x=45°，即∠A=45°．

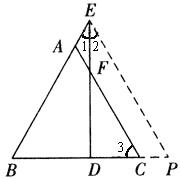
例4、数学课堂上，老师布置了一道几何证明题，让大家讨论它的证明方法，通过大家的激烈讨论，有几位同学说出了他们的思路，并添加了辅助线，你能根据他们的辅助线的作法写出证明过程吗？

　　如图，已知△ABC中AB=AC，F在AC上，在BA延长线上取AE=AF．求证：EF⊥BC．

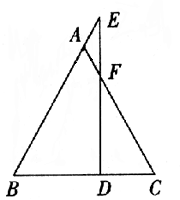
解：

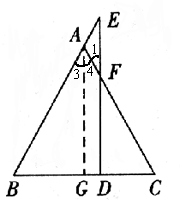
　　首先，小明根据等腰三角形这一已知条件，结合等腰三角形的性质，想到了过A作AG⊥BC于G这一条辅助线，如图．

证明1：

　　过A作AG⊥BC于G．

　　∵AB=AC，∴∠3=∠4．

　　又∵AE=AF，∴∠1=∠E．

　　又∵∠3＋∠4=∠1＋∠E，

　　∴∠3=∠E，

　　∴AG//EF，

　　∴EF⊥BC．

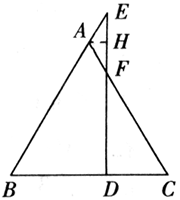
　　接着小亮根据题设AE=AF，结合等腰三角形的性质作出过A作AH⊥EF于H这条辅助线，如图．

证明2：

　　过A作AH⊥EF于H．

　　∵AE=AF，∴∠EAH=∠FAH．

　　又∵∠AB=AC，∴∠B=∠C．

　　又∵∠EAH＋∠FAH=∠B＋∠C，

　　∴∠EAH=∠B，

　　∴AH//BC，

　　∴EF⊥BC．

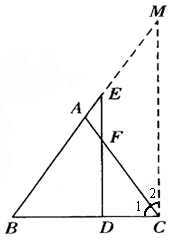
　　小彬也作出了一条辅助线，过C作MC⊥BC交BA的延长线于M，如图．

证明3：

　　过C作MC⊥BC交BA的延长线于M，则∠1＋∠2=90°．

　　∵AE=AF，∴∠AEF=∠AFE，

　　∴∠EAF=180°－2∠AFE．

　　又∵AB=AC，∴∠B=∠1．

　　又∵∠EAF=∠B＋∠1，∴∠EAF=2∠1，

　　∴2∠1=180°－2∠AFE，

　　∴∠1＋∠AFE=90°，

　　∴∠2=∠AFE，

　　∴DE//MC，

　　∴EF⊥BC．

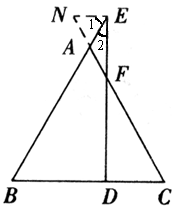
　　小颖的作法是：过E作EN⊥EF交CA的延长线于N，如图．

证明4：

　　过E作EN⊥EF交CA的延长线于N，则∠1＋∠2=90°．

　　∵AE=AF，

　　∴∠2=∠AFE，∴∠EAF=180°－2∠2．

　　又∵AB=AC，∴∠B=∠C，∴∠EAF=∠B＋∠C=2∠B，

　　∴2∠B=180°－2∠2，∴∠B＋∠2=90°，

　　∴∠1=∠B，∴EN//BC，

　　∴EF⊥BC．

　　小虎的作法是：过E点作EP//AC交BC的延长线于P，如图．

证明5：

　　过E作EP//AC交BC的延长线于P，则∠AFE=∠2，∠3=∠P．

　　又∵AE=AF，∴∠1=∠AFE，

　　∴∠1=∠2．

　　又∵AB=AC，∴∠B=∠3，

　　∴∠B=∠P，∴EB=EP，

　　∴EF⊥BC．

　　大家都在激烈地讨论着如何作出辅助线时，小红突然站起来说，不作辅助线也可以证明，你说是吗？（如图）．

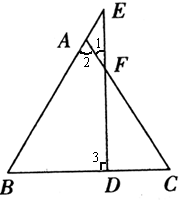
证明6：

　　∵AE=AF，∴∠1=∠E．

　　又∵∠2=∠1＋∠E，

　　∴∠2=2∠E．

　　又∵AB=AC，∴∠B=∠C，

　　∴∠2=180°－2∠B，

　　∴2∠E=180°－2∠B，

　　即∠E＋∠B=90°，

　　∴∠3=180°－90°=90°，

　　∴EF⊥BC．

例5、如图所示，在△ABC中，AB=AC，∠BPC=115°，且∠ABP=∠BCP，求∠A的度数．

分析：

　　可以利用整体的数学思想，设∠ABP=∠BCP=α，则∠PBC=∠ACP=β，

　　因为AB=AC，所以∠ABC=∠ACB，即∠A=180°－∠ABC－∠ACB=180°－2(α＋β)，△BCP中，α＋β=180－∠BPC，故可求出∠A的度数。

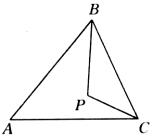
解：

　　∵AB=AC，∴∠ABC=∠ACB（等边对等角）。

　　又∵∠ABP=∠BCP，

　　∴∠ABC－∠ABP=∠ACB－∠BCP，即∠PBC=∠ACP。

　　设∠ABP=∠BCP=α，∠PBC=∠ACP=β。

　　在△BCP中，∠BPC=180°－α－β，∠BPC=115°，∴α＋β=65°。

　　∴∠A=180°－2(α＋β)=180°－2×65°=50°。

例6、如图所示，∠AOP=∠BOP=15°，PD⊥OA，PC∥OD，若OC=4，则PD等于（　）

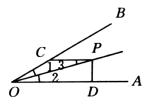
A．4　　　　　B．3　　　　　C．2　　　　　　D．1

分析：

　　本题中有角平分线、平行线，这是等腰三角形的重要形成条件，另外PD⊥OA于D，显然需要作另外一个垂直，这是角平分线性质的重要应用。具体证明过程如下：

　　如图所示，过点P作PE⊥OB于E。

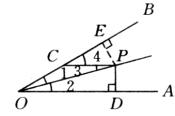
　　∵OP平分∠BOA，PD⊥OA于D，

　　∴PD=PE，∠1=∠2。

　　∵PC∥OA，∴∠2=∠3，∴∠1=∠3，∴OC=CP=4。

　　又∵∠1=15°，∴∠4=∠1＋∠3=30°，

　　

　　故正确答案为C项。

- 返回 -