例1、（ ）如图所示，已知在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F，试说明：BF=2CF。

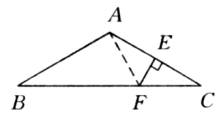
分析：

　　由线段垂直平分线想到连结FA，再设法找到具有30°角的直角三角形，证明线段的2倍关系。

解：

　　连结AF，∴EF是AC的垂直平分线，

　　∴FA=FC，∴∠C=∠FAC。

　　又∵∠BAC=120°，∴∠B＋∠C=60°。

　　又∵AB=AC，∴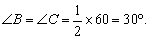

　　∴在∠BAF=∠BAC－∠FAC=120°－30°=90°。

　　在Rt△ABF中，∠BAF=90°，∠B=30°，

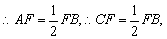　　即BF=2CF。

例2、（宜宾）如图，直角ΔABC中,∠ACB=90°,∠A=15°，将顶点A翻折使它与顶点B重合，折痕为MH，已知AH=2，那么BC=_____________．

分析：

　　折叠问题可以看成轴对称问题．由外角定理得到直角三角形中有30°角，利用30°角所对的直角边等于斜边的一半可得．

解：

　　由于轴对称，得∠MA′H=∠A=15°，

　　所以∠BHC=30°，BH=AH，

　　又△BHC为直角三角形，因为直角三角形中30°角所对的直角边等于斜边的一半，

　　所以 BC=BH=×2=1．

 

-END-