一、选择题

1、如图，∠A=15°，AB=BC=CD=DE=DF，则∠DEF为（　）

A．90°　　　　　　　　　　　　　　　B．75°

C．70°　　　　　　　　　 　　　　　 D．60°

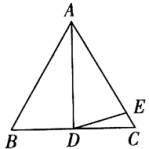
2、如图，△ABC中，AB=AC，∠BAD=30°，且AD=AE，则∠EDC等于（　）

A．15°　　　　　　　　　　　　　　　B．20°

C．25°　　　　　　　　　　　　　　　D．30°

3、已知等腰三角形ABC的底边BC=8cm，且|AC－BC|=2cm，则腰AC的长为（　）

A．10cm或6cm　　　　　　　　　　　　 B．10cm

C．6cm　　　　　　　　　　　　　　　 D．8cm或6cm

4、等腰三角形的一边等于5，一边等于12，则它的周长为（　）

A．22　　　　　　　　　　　　　　　　B．29

C．22或29　　　　　　　　　　　　　　D．17

5、如图，D、E分别是△ABC的边BC、AC上的点，若AB=AC，AD=AE，则（　）

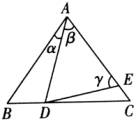
A．当∠B为定值时，∠CDE为定值

B．当∠α为定值时，∠CDE为定值

C．当∠β为定值时，∠CDE为定值

D．当∠γ为定值时，∠CDE为定值

6、如图，在△ABC中，AB=AC，BF=CD，BD=CE，∠FDE=α，则下列结论正确的是（　）

A．2α＋∠A=180°　　　　　　　　　　B．α＋∠A=90°

C．2α＋∠A=90°　　　　　　　　　　 D．α＋∠A=180°

7、如图，在△ABC中，∠B=2∠C，则AC与2AB之间的关系是（　）

A．AC>2AB　　　　　　　　　　　　　　B．AC=2AB

C．AC≤2AB　　　　　　　　　　　　　 D．AC＜2AB

8、等边三角形两条中线所组成的钝角的度数是（　）

A．120°　　　　　　　　　　　　　　 B．130°

C．150°　　　　　　　　　　　　　　 D．160°

9、三角形中有一条边是另一条边的2倍，并且有一个内角是30°，那么这个三角形（　）

A．一定是直角三角形　　　　　　　　　B．一定是钝角三角形

C．可能是锐角三角形　　　　　　　　　D．不可能是锐角三角形

10、如图，两个全等的直角三角形中都有一个锐角为30°，且较长的直角边在同一直线上，则图中的等腰三角形有（　）

A．4个　　　 　　　　　　　　　　　　B．3个

C．2个　　　　　　　　　　　　　　　 D．1个