解三元一次方程组和二元一次方程组基本方法一样，仍然是消元，其基本方法也是代入消元法和加减消元法，
3、解三元一次方程组的一般步骤：
（1）利用代入法和加减法，消去一个未知数，得出一个二元一次方程组；
（2）解这个二元一次方程组，求得两个未知数的值；
（3）将这两个未知数的值代入原方程组中较简单的一个方程，求出第三个未知数的值，把这三个未知数的值写在一起就是所求三元一次方程组的解．
1、三元一次方程组的解法和基本思想与解二元一次方程组相同，仍是用代入法或加减法消元，即通过消元将三元一次方程组转化为二元一次方程组，再转化为一元一次方程．
2、如何消元．如同解二元一次方程组．首先要认真观察方程组中各方程中系数的特点，可根据题目的特点，然后选择最好的解法，灵活消元．
3、有些特殊方程组，可用特殊的消元方法，有时一下子可消去两个未知数，直接求出一个未知数值来．
4、解一次方程组的消元“转化”基本思想，可以推广到“四元”、“五元”等多元方程组．
例1、解方程组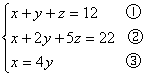
分析：
方程③是关于x的表达式，通过代入消元法可直接转化为二元一次方程组，因此确定“消x”的目标．
解法1：
代入法，消x.
把③分别代入①、②得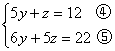
解得
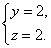
把y＝2代入③，得x＝8.
因此三元一次方程组的解为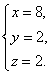
观察方程组进行分析，方程组中的方程③里缺z，因此利用①、②消z，也能达到消元构成二元一次方程组的目的．
解法2：消z.
①×5得 5x＋5y＋5z＝60 ④
④－② 得4x＋3y＝38 ⑤
由③、⑤得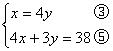
解得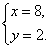
把x＝8，y＝2代入①得z＝2.
因此三元一次方程组的解为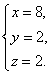
点评：
解法一根据方程组中有表达式，可用代入法消元.解法二根据方程组中③缺z元，可由①②消去z元得关于x，y的方程组.
例2、解方程组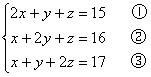
.
分析：
通过观察发现每个方程未知项的系数和相等；每一个未知数的系数之和也相等，即系数和相等．具备这种特征的方程组，我们给它定义为“轮换方程组”，可采取求和作差的方法较简洁地求出此类方程组的解．
解：
由①＋②＋③得4x＋4y＋4z＝48，
即x＋y＋z＝12 .④
①－④得 x＝3，
②－④得 y＝4，
③－④得 z＝5，
因此三元一次方程组的解为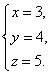
小结：轮换方程组，采用求和作差法.
例3、解方程组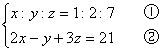
分析1：
观察此方程组的特点是未知项间存在着比例关系，根据以往的经验，见比例式就会想把比例式化成关系式求解，即由x∶y＝1∶2得y＝2x； 由x∶z＝1∶7得z＝7x.从而从形式上转化为三元一次方程组的一般形式，即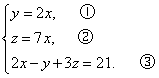
，根据方程组的特点，可选用“有表达式，用代入法”求解．
解法1：
由①得y＝2x，z＝7x ，并代入②，得x＝1.
把x＝1，代入y＝2x，得y＝2；
把x＝1，代入z＝7x，得 z＝7.
因此三元一次方程组的解为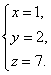
分析2：
由以往知识可知遇比例式时，可设一份为参数k，因此由方程①x︰y︰z＝1︰2︰7，可设为x＝k，y＝2k，z＝7k.从而也达到了消元的目的，并把三元通过设参数的形式转化为一元，可谓一举多得．
解法2：
由①设x＝k，y＝2k，z＝7k，并代入②，得k＝1.
把k＝1，代入x＝k，得x＝1；
把k＝1，代入y＝2k，得y＝2；
把k＝1，代入z＝7k，得 z＝7.
因此三元一次方程组的解为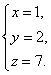
小结：遇比例式找关系式，采用设元解法.
例4、解方程组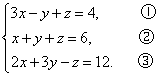
分析：
对于一般形式的三元一次方程组的求解，应该认清两点：一是确立消元目标——消哪个未知项；二是在消元的过程中三个方程式如何正确的使用，怎么才能做到“目标明确，消元不乱”．
解：
①＋③ 得5x＋2y＝16，④
②＋③ 得3x＋4y＝18，⑤
由④、⑤得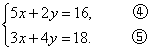
解得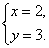
把x＝2，y＝3代人②，得 z＝1.
因此三元一次方程组的解为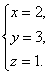
小结：
一般选择同一个未知项系数相同或互为相反数的那个未知数消元；或选择同一个未知项系数最小公倍数最小的那个未知数消元．
例5、学校的篮球数比排球数的2倍少3个，足球数与排球数的比是2∶3，三种球共41个，求三种球各有多少个？
分析：
设篮球数为x个，排球数为y个，足球数为z个，分析题中存在的相等关系：
①篮球数＝2×排球数－3，即x＝2y－3；
②足球数：排球数＝2∶3，即z∶y＝2∶3；
③三种球数的总和为41个，即x＋y＋z＝41.
解：设篮球有x个，排球有y个，足球有z个，
依题意，得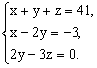
解这个方程组，得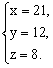
答：篮球有21个，排球有12个，足球有8个.
