(一)相对论
1、爱因斯坦通过对电磁理论的深入研究,于1905年提出了两个基本假设:
(1)相对性原理:物理规律在一切惯性参照系中都具有相同的形式。
(2)光速不变原理:在一切惯性参照系中,测量到的真空中的光速c都一样。
相对性原理表明:在某个惯性系中,描述某个物理系统的某个物理过程的物理定律,在其他一切惯性系中对该系统该过程做出描述的物理定律皆保持形式不变。
光速不变原理表明:在一切惯性系中观测在真空中传播的同一束光,不论沿任何方向,其速度大小都为c,与光源或观察者的运动无关。这一结论实际上已被大量的实验(包括迈克尔逊实验)证实。
基于这两条基本原理,爱因斯坦建立了狭义相对论。
2、时间延缓效应
在相对论时空观中,△t与△t′不相等,它们之间的关系为
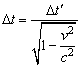
由于v是列车的速度,且v<c,由上式可知,△t>△t′。因此,如果某时钟所显示的某个物理过程经历的时间间隔小,我们就称该时钟走得慢。所以我们说运动的钟(如上述车里的钟)比静止的钟(如上述地面的钟)走得慢。这种效应被称为时间延缓。
3、长度收缩效应
经典时空观认为,空间(包括物体的长、宽、高)与运动无关。
按照狭义相对论时空观,空间也与运动密切相关,即对某物体空间广延性的观测,与观测者和该物体的相对运动有关。
4、质量的变化
但是基于相对论和其他物理原理,可推出物质的质量是变化的。当物体在所处的惯性参照系静止时,它具有最小的质量m0,这个质量叫做静止质量。当物体以速度v相对某惯性系运动时,在这个惯性系观测它的质量为
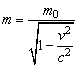
可见,在某个惯性系中观测某个物体,它的质量观测值会随着它运动速度的增大而增大。
一个真实的物质,其质量是确定值、有限大,所以按相对论来讲,一个真实的、静止质量不为零的物体,相对任何惯性系的运动速度都不可能等于或超过光速c。
对于低速运动的物体,质量的变化完全可以忽略不计。
5、质能公式
在经典物理学中,质量和能量是两个独立的概念。按照相对论及基本力学定律可推出质量和能量具有如下关系
E=mc2
这就是著名的质能关系式。式中,m是物质的质量,单位是kg;c是真空中的光速,单位是m/s;E是物质的能量,单位是J。质量和能量是物质不可分离的属性。当物质的质量减少或增加时,必然伴随着能量的减少或增加。如果用△m表示物体质量的变化量,△E表示能量的变化量,那么它们的关系可以表示为
△E=△mc2
该式表示,随着一个物体质量的减少,会释放出一定的能量;与此同时,另一个物体吸收了能量,质量也会随之增加。
某个静质量为m0的物体,相对它静止的观测者测其质量为m=m0;能量为E=mc2=m0c2,记为E0=m0c2,称为静能量。
这表明任何静质量不为零的物体,都贮存着巨大的能量。
当某物体受到高能量的作用而发生静质量转化△m0时,就会释放出巨大的能量△E0=△m0c2。
哈恩的重核裂变反应,使爱因斯坦的质能关系得到了验证和实现。
6、时空弯曲效应
爱因斯坦基于广义相对论时空观和经典的牛顿引力场理论,最终提出广义相对论引力场方程。
(二)量子论
1、普朗克的量子假说
普朗克的量子假说认为,物质辐射(或吸收)的能量E只能是某一最小能量单位的整数倍。
E=nε n=0,1,2,3,…
辐射是由一份份的能量组成的,就像物质是由一个个原子组成的一样。辐射中的一份能量就是一个量子。量子的能量大小取决于辐射的波长,量子的能量ε与波长λ成反比,与频率v成正比。
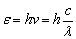
公式中的h是普朗克常数,数值为6.626176×10-34J·S,这是普朗克引进的一个物理普适常数,它是微观现象量子特性的表征。
2、物质的波粒二象性
有两种有关光的本性的认识:光的波动性和光的粒子性。
(1)牛顿是光的微粒学说的创始人。牛顿认为,光是从光源射出的具有高速度的粒子流。微粒学说可以解释光的反射、光的颜色等,因此在18世纪粒子说得到许多人的认可。但是,微粒说不能解释光的干涉、衍射等现象。荷兰物理学家惠更斯认为,光像水波一样,也是一种波,叫光波。19世纪60年代,英国物理学家麦克斯韦创立的经典电磁场理论提示出:光是一种电磁波。因此到19世纪,波动说才代替微粒说,得到大家的承认。
到20世纪,由于光电效应的出现,人们发现用电磁波来解释这一效应又出现困难,这就触发了人们对光的本质的再认识。
(2)光量子假设。爱因斯坦认为,光是不连续的、分成许多单元的、具有一定能量的物质,这些单元叫做光量子。
1922年,康普顿效应的发现才最终令人信服地验证了光量子假说的正确性,使光量子概念开始为人们所接受。随后,光量子正式被命名为光子(photon)。
(3)光具有波粒二象性。它在一定的条件下,突出地表现出微粒性,实质为不连续性;而在另一些条件下,又突出地表现出波动性。
(4)法国物理学家德布罗意通过研究、分析、类比,意识到既然光具有波粒二象性,那么静质量不为零的物质粒子(如电子)也应当具有波的性质。德布罗意进一步提出了物质波理论,根据这一理论,每个物质粒子都伴随着一种波,这种波被称为物质波,又称为概率波。德布罗意理论提示了物质(包括光和电子)的统一性。
物质波的假说一经提出,很快就为一系列实验证实
(三)典型例题
例1、下列说法正确的是( )
A.光波是一种概率波
B.光波是一种电磁波
C.单色光从光密介质进入光疏介质时,光子的能量改变
D.单色光从光密介质进入光疏介质时,光的波长不变
分析:从光的波粒二象性可知光波是一种概率波。光子说可知光子能量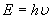 不同介质中光的频率保持不变,由
不同介质中光的频率保持不变,由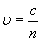 可得
可得
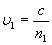 ;
;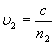 ,所以:
,所以: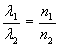
因此,波长在不同介质中是不同的,正确答案A、B
解答:AB
评注:本题主要考查光的常识,解题关键是把握好光的波粒二象性
例2、下列说法正确的是( )
A.光的干涉和衍射现象说明光具有波动性
B.光的频率越大波长越长
C.光的波长越大,光子能量越大
D.光在真空中的传播速度为3.00×108 m/s
分析:干涉和衍射是波所特有的现象。光的干涉和衍射现象说明光具有波动性,A正确。光的波长由光速和频率共同决定,B错误,由光子的能量E=hv,可知,光的波长越长,光子能量越小,C错误,光在真空中的传播速度等于光速为3×108 m/s,D正确。
解答:AD
评注:本题主要考查光的本性,光的波粒二象性与光速是本考点的热点命题方向。解题时应注意光的反射、折射、干涉、衍射等现象说明光具有波动性,光是一份一份不连续的光子,又具有微粒性。
例3、分别用波长为λ和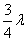 的单色光照射同一金属板,发出的光电子的最大初动能之比为1:2,以h表示普朗克常数c表示真空中的光速,则此金属板的逸出功为:( )
的单色光照射同一金属板,发出的光电子的最大初动能之比为1:2,以h表示普朗克常数c表示真空中的光速,则此金属板的逸出功为:( )
A.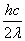 B.
B.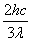
C.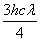 D.
D.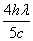
分析: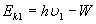 ;
;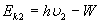
两式相比可得:W=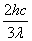 ;所以B正确。
;所以B正确。
评注:主要考查爱因斯坦光电方程。
例4、下表给出了一些金属材料的逸出功。
材料 |
铯 |
钙 |
镁 |
铍 |
钛 |
逸出功(10-19J) |
3.0 |
4.3 |
5.9 |
6.2 |
6.6 |
现用波长为400 nm的单色光照射上述材料能产生光电效应的材料最多有几种(普朗克常数h=6.6×10-34J·s,光速c=3×108 m/s)( )
A.2种 B.3种
C.4种 D.5种
分析:先求出单色光的光子能量,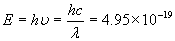 J,再将该数值与表中各种金属的逸出功进行比较,可得出能产生光电效应的有铯、钙两种。
J,再将该数值与表中各种金属的逸出功进行比较,可得出能产生光电效应的有铯、钙两种。
解答:A
评注:本题考查的是光电效应,涉及逸出功、光子能量及产生光电效应的条件等知识,解答该题的切入点就是发生光电效应的条件即入射光子的能量大于金属的逸出功。
例5、在光的双缝干涉实验中,在光屏上放上照相底片,并设法减弱光的强度,使光子只能一个一个的通过狭缝,设每个光子在狭缝上通过打在底处上就留下一点,则( )
A.若曝光时间不太长,则在底片上出现一些无规则的点
B.若曝光时间足够长,则底片上出现干涉条纹
C.这实验表明光具有粒子性
D.这一实验结果表明光具有波动性
分析:光具波粒二象性,大量光子表现为波动性,个别光子物质产生作用时往往表现为粒子性,所以A、B、C正确。
答案:ABC
评注:在光的双缝干涉实验中,如果短时间曝光,发现光子在底片上呈现不规则分布的点子,长时间曝光才形成明暗相间的条纹。这说明了光的波动性不同于机械波,也不同于经典意义下的电磁波,而是一种概率波,即表现为光子在空间各点出现的可能性的大小。所谓概率大,即出现光子的数目多,也就是干涉、衍射时呈现出明亮的条纹;所谓概率小,即光子出现的数目少,也就是干涉、衍射时呈现出较暗的条纹。
例6、计算波长是0.1220微米的紫外线的光子的能量,用焦耳和电子伏两种单位表示。
分析:根据光子说光子能量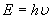
解答: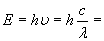
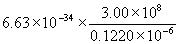 J
J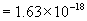 J
J
即是: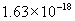 J=10.2eV
J=10.2eV