![]() 8.6.3 平面与平面垂直
8.6.3 平面与平面垂直
![]()
考点 | 学习目标 | 核心素养 |
二面角 | 理解二面角的有关概念,会求简单的二面角的大小 | 直观想象、数学运算 |
平面与平面垂直的判定定理 | 理解两平面垂直的定义,掌握两平面垂直的判定定理 | 直观想象、逻辑推理 |
平面与平面垂直的性质定理 | 理解平面和平面垂直的性质定理,并能用文字、符号 和图形语言描述定理,能应用面面垂直的性质定理 解决有关的垂直问题 | 直观想象、逻辑推理 |
![]()
![]() 问题导学
问题导学
预习教材P155-P161的内容,思考以下问题:
1.二面角的定义是什么?
2.如何表示二面角?
3.二面角的平面角的定义是什么?
4.二面角的范围是什么?
5.面面垂直是怎样定义的?
6.面面垂直的判定定理的内容是什么?
7.面面垂直的性质定理的内容是什么?
![]()
1.二面角
(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
(2)图形和记法
图形:
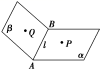
记作:二面角αABβ或二面角αlβ或二面角PABQ或二面角PlQ.
2.二面角的平面角
(1)定义:在二面角αlβ的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.
(2)图形、符号及范围
图形:
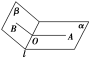
符号:OA⊥l,OB⊥l⇒∠AOB是二面角的平面角.
范围:0°≤∠AOB≤180°.
(3)规定:二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.平面角是直角的二面角叫做直二面角.
■名师点拨
(1)二面角的大小与垂足O在l上的位置无关.一个二面角的平面角有无数个,它们的大小是相等的.
(2)构成二面角的平面角的三要素:“棱上”“面内”“垂直”.即二面角的平面角的顶点必须在棱上,角的两边必须分别在两个半平面内,角的两边必须都与棱垂直,这三个条件缺一不可.这三个要素决定了二面角的平面角大小的唯一性和平面角所在的平面与棱垂直.
3.平面与平面垂直
(1)定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β.
(2)判定定理
文字语言 | 图形语言 | 符号语言 |
如果一个平面过另一个平面的垂线,那么这两个平面垂直 |
| l⊂α⇒α⊥β |
■名师点拨
定理的关键词是“过另一个平面的垂线”,所以应用的关键是在平面内寻找另一个平面的垂线.
4.平面与平面垂直的性质定理
文字语言 | 两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直 |
符号语言 | a⊥l⇒a⊥β |
图形语言 |
|
作用 | ①面面垂直⇒线面垂直 ②作面的垂线 |
■名师点拨
对面面垂直的性质定理的理解
(1)定理的实质是由面面垂直得线面垂直,故可用来证明线面垂直.
(2)已知面面垂直时,可以利用此定理转化为线面垂直,再转化为线线垂直.
![]()
![]() 判断(正确的打“√”,错误的打“×”)
判断(正确的打“√”,错误的打“×”)
(1)二面角的平面角的大小与其顶点在二面角棱上的位置有关.( )
(2)二面角可以看成是一个半平面以其棱为轴旋转而成的.( )
(3)如果平面α内有一条直线垂直于平面β内的一条直线,则α⊥β.( )
(4)如果两个平面垂直,那么一个平面内的直线一定垂直于另一个平面.( )
(5)如果两个平面垂直,那么垂直于交线的直线必垂直于其中一个平面.( )
答案:(1)× (2)√ (3)× (4)× (5)×
![]() 在二面角αlβ的棱l上任选一点O,若∠AOB是二面角αlβ的平面角,则必须具有的条件是( )
在二面角αlβ的棱l上任选一点O,若∠AOB是二面角αlβ的平面角,则必须具有的条件是( )
A.AO⊥BO,AO⊂α,BO⊂β
B.AO⊥l,BO⊥l
C.AB⊥l,AO⊂α,BO⊂β
D.AO⊥l,BO⊥l,且AO⊂α,BO⊂β
答案:D
![]() 已知直线l⊥平面α,则经过l且和α垂直的平面( )
已知直线l⊥平面α,则经过l且和α垂直的平面( )
A.有1个 B.有2个
C.有无数个 D.不存在
答案:C
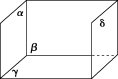
![]() 若平面α⊥平面β,平面β⊥平面γ,则( )
若平面α⊥平面β,平面β⊥平面γ,则( )
A.α∥γ B.α⊥γ
C.α与γ相交但不垂直 D.以上都有可能
解析:选D.由题意知,α与γ可能平行,也可能相交.如图,α与δ平行,α与γ相交.
![]() 如图,P是二面角αlβ内的一点,PA⊥α,PB⊥β,垂足分别为A,B.若∠APB=80°,则二面角αlβ的大小为 W.
如图,P是二面角αlβ内的一点,PA⊥α,PB⊥β,垂足分别为A,B.若∠APB=80°,则二面角αlβ的大小为 W.
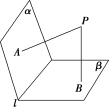
答案:100°
![]()
![]()
二面角的概念及其大小的计算
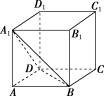
![]() (1)在正方体ABCDA1B1C1D1中,截面A1BD与底面ABCD所成锐二面角A1BDA的正切值为( )
(1)在正方体ABCDA1B1C1D1中,截面A1BD与底面ABCD所成锐二面角A1BDA的正切值为( )
A.2 B.2
C. D.
(2)一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角的大小关系为( )
A.相等 B.互补
C.相等或互补 D.不确定
【解析】 (1)如图所示,连接AC交BD于点O,连接A1O,O为BD的中点,因为A1D=A1B,所以在△A1BD中,A1O⊥BD.
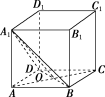
又因为在正方形ABCD中,AC⊥BD,所以∠A1OA为二面角A1BDA的平面角.
设AA1=1,则AO=2.所以tan∠A1OA=2=.
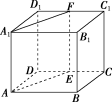 (2)反例:如图,在正方体ABCDA1B1C1D1中,E,F分别是CD,C1D1的中点,二面角DAA1E与二面角B1ABC的两个半平面就是分别对应垂直的,但是这两个二面角既不相等,也不互补.
(2)反例:如图,在正方体ABCDA1B1C1D1中,E,F分别是CD,C1D1的中点,二面角DAA1E与二面角B1ABC的两个半平面就是分别对应垂直的,但是这两个二面角既不相等,也不互补.
【答案】 (1)C (2)D

(1)求二面角大小的步骤

简称为“一作二证三求”.
(2)作出二面角的平面角的方法
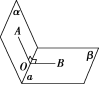 方法一:(定义法)在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.
方法一:(定义法)在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.
如图所示,∠AOB为二面角αaβ的平面角.
 方法二:(垂线法)过二面角的一个面内一点作另一个平面的垂线,过垂足作棱的垂线,连接该点与垂足,利用线面垂直可找到二面角的平面角或其补角.
方法二:(垂线法)过二面角的一个面内一点作另一个平面的垂线,过垂足作棱的垂线,连接该点与垂足,利用线面垂直可找到二面角的平面角或其补角.
如图所示,∠AFE为二面角ABCD的平面角.
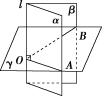 方法三:(垂面法)过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角即为二面角的平面角.
方法三:(垂面法)过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角即为二面角的平面角.
如图所示,∠AOB为二面角αlβ的平面角.
[提醒] 二面角的平面角的大小与顶点在棱上的位置无关,通常可根据需要选择特殊点作平面角的顶点.
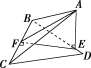
![]() 若P是△ABC所在平面外一点,而△PBC和△ABC都是边长为2的正三角形,PA=,那么二面角PBCA的大小为 W.
若P是△ABC所在平面外一点,而△PBC和△ABC都是边长为2的正三角形,PA=,那么二面角PBCA的大小为 W.
解析:如图,取BC的中点O,连接OA,OP,则∠POA为二面角PBCA的平面角,OP=OA=,PA=,所以△POA为直角三角形,∠POA=90°.
答案:90°
![]()
平面与平面垂直的判定
角度一 利用定义证明平面与平面垂直
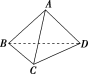
![]() 如图,在四面体ABCD中,BD=a,AB=AD=CB=CD=AC=a.求证:平面ABD⊥平面BCD.
如图,在四面体ABCD中,BD=a,AB=AD=CB=CD=AC=a.求证:平面ABD⊥平面BCD.
【证明】 因为△ABD与△BCD是全等的等腰三角形,
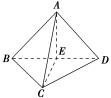 所以取BD的中点E,连接AE,CE,则AE⊥BD,BD⊥CE.
所以取BD的中点E,连接AE,CE,则AE⊥BD,BD⊥CE.
在△ABD中,AB=a,
BE=2BD=2a,
所以AE= =2a.
同理CE=2a,在△AEC中,
AE=CE=2a,AC=a.
由于AC2=AE2+CE2,
所以AE⊥CE,∠AEC是二面角ABDC的平面角,又因为∠AEC=90°,
所以二面角ABDC为直二面角,
所以平面ABD⊥平面BCD.
角度二 利用判定定理证明平面与平面垂直
![]()
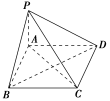 如图,在四棱锥PABCD中,若PA⊥平面ABCD且四边形ABCD是菱形.求证:平面PAC⊥平面PBD.
如图,在四棱锥PABCD中,若PA⊥平面ABCD且四边形ABCD是菱形.求证:平面PAC⊥平面PBD.
【证明】 因为PA⊥平面ABCD,
BD⊂平面ABCD,
所以BD⊥PA.
因为四边形ABCD是菱形,
所以BD⊥AC.
又PA∩AC=A,
所以BD⊥平面PAC.
又因为BD⊂平面PBD,
所以平面PAC⊥平面PBD.
![]()
证明平面与平面垂直的两种常用方法
(1)利用定义:证明二面角的平面角为直角,其判定的方法是:
①找出两相交平面的平面角;
②证明这个平面角是直角;
③根据定义,这两个相交平面互相垂直.
(2)利用面面垂直的判定定理:要证面面垂直,只要证线面垂直.即在其中一个平面内寻找一条直线与另一个平面垂直.这是证明面面垂直的常用方法,其基本步骤是:
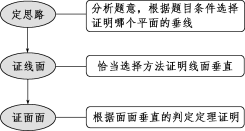
![]() 如图所示,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=2PD.证明:平面PQC⊥平面DCQ.
如图所示,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=2PD.证明:平面PQC⊥平面DCQ.
证明:由四边形ABCD为正方形,可得CD⊥AD,
又PD⊥平面ABCD,
所以PD⊥CD,PD⊥AD,
 故CD⊥平面AQPD,从而CD⊥PQ.
故CD⊥平面AQPD,从而CD⊥PQ.
如图所示,取PD的中点E,连接QE.因为PD∥QA,QA=2PD,则DE∥AQ,且DE=AQ,
从而四边形AQED是平行四边形,
则QE∥AD,所以QE⊥PD,
所以DQ=QP.
设QA=1,则AB=1,PD=2.
在△DQP中,
有DQ=QP=,PD=2.
所以DQ2+QP2=PD2,
故∠PQD=90°,即DQ⊥PQ.
又CD∩DQ=D,
所以PQ⊥平面DCQ.
又PQ⊂平面PQC,
所以平面PQC⊥平面DCQ.
![]()
面面垂直的性质定理的应用
![]() 已知P是△ABC所在平面外的一点,且PA⊥平面ABC,平面PAC⊥平面PBC,求证:BC⊥AC.
已知P是△ABC所在平面外的一点,且PA⊥平面ABC,平面PAC⊥平面PBC,求证:BC⊥AC.
【证明】 如图,在平面PAC内作AD⊥PC于点D,
因为平面PAC⊥平面PBC,平面PAC∩平面PBC=PC,AD⊂平面PAC,且AD⊥PC,
所以AD⊥平面PBC,
又BC⊂平面PBC,所以AD⊥BC.
因为PA⊥平面ABC,BC⊂平面ABC,
所以PA⊥BC,
因为AD∩PA=A,
所以BC⊥平面PAC,
又AC⊂平面PAC,所以BC⊥AC.
![]()
利用面面垂直的性质定理应注意的问题
若所给题目中有面面垂直的条件,一般要利用面面垂直的性质定理将其转化为线面垂直、线线垂直.应用面面垂直的性质定理,应注意三点:①两个平面垂直是前提条件;②直线必须在其中一个平面内;③直线必须垂直于它们的交线.
![]()
 如图,△ABC是正三角形,若AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,求证:AE∥平面BCD.
如图,△ABC是正三角形,若AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,求证:AE∥平面BCD.
证明:如图,取BC的中点M,
连接DM,AM,
 因为BD=CD,
因为BD=CD,
所以DM⊥BC.
又因为平面BCD⊥平面ABC,
DM⊂平面BCD,两平面交线为BC,
所以DM⊥平面ABC,
又AE⊥平面ABC,
所以AE∥DM.
又因为AE⊄平面BCD,DM⊂平面BCD,
所以AE∥平面BCD.
![]()
垂直关系的综合问题
![]()
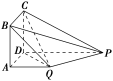
 如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:
(1)DE=DA;
(2)平面BDM⊥平面ECA;
(3)平面DEA⊥平面ECA.
【证明】 (1)如图,取EC的中点F,连接DF.
因为EC⊥平面ABC,BC⊂平面ABC,
所以EC⊥BC.
同理可得BD⊥AB,
易知DF∥BC,所以DF⊥EC.
在Rt△EFD和Rt△DBA中,
因为EF=2EC,EC=2BD,
 所以EF=BD.
所以EF=BD.
又FD=BC=AB,
所以Rt△EFD≌Rt△DBA,故DE=DA.
(2)取CA的中点N,连接MN,BN,
则MN∥EC,且MN=2EC.
因为EC∥BD,BD=2EC,
所以MN綊BD,
所以N点在平面BDM内.
因为EC⊥平面ABC,
所以EC⊥BN.
又CA⊥BN,EC∩CA=C,所以BN⊥平面ECA.
因为BN在平面MNBD内,
所以平面MNBD⊥平面ECA,
即平面BDM⊥平面ECA.
(3)由(2)易知DM∥BN,BN⊥平面ECA,
所以DM⊥平面ECA.
又DM⊂平面DEA,
所以平面DEA⊥平面ECA.
![]()
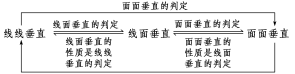
垂直关系的转化
在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化.每一种垂直的判定都是从某一垂直开始转向另一垂直,最终达到目的,其转化关系如下:
![]() 如图,在四棱锥PABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.求证:
如图,在四棱锥PABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.求证:
(1)PA⊥底面ABCD;
(2)BE∥平面PAD;
(3)平面BEF⊥平面PCD.
证明:(1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.
(2)因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE.
所以四边形ABED为平行四边形.所以BE∥AD.
又因为BE⊄平面PAD,AD⊂平面PAD,
所以BE∥平面PAD.
(3)因为AB⊥AD,而且四边形ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD,
所以PA⊥CD.
又PA∩AD=A,所以CD⊥平面PAD.
所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PD∥EF.所以CD⊥EF.
又因为CD⊥BE,EF∩BE=E,
所以CD⊥平面BEF.
因为CD⊂平面PCD,
所以平面BEF⊥平面PCD.
![]()
1.给出以下四个命题,其中真命题的个数是( )
①如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行;
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面;
③如果两条直线都平行于一个平面,那么这两条直线相互平行;
④如果一个平面经过另一个平面的一条垂线,那么这两个平面相互垂直.
A.4 B.3
C.2 D.1
解析:选B.①②④正确.①线面平行的性质定理;②线面垂直的判定定理;③这两条直线可能相交或平行或异面;④面面垂直的判定定理.
2.在下列关于直线m,l和平面α,β的说法中, 正确的是( )
A.若l⊂β,且α⊥β,则l⊥α
B.若l⊥β,且α∥β,则l⊥α
C.若l⊥β,且α⊥β,则l∥α
D.若α∩β=m,且l∥m,则l∥α
解析:选B.A项中l与α可以平行或斜交,A项错.
B项中,l⊥β且α∥β,所以l⊥α正确.
C项中,l可在α内,C项错.
D项中,l可在α内,D项错.
3.在三棱锥PABC中,PA=PB=AC=BC=2,PC=1,AB=2,则二面角PABC的大小为 W.
解析: 取AB的中点M,连接PM,MC,则PM⊥AB,CM⊥AB,
取AB的中点M,连接PM,MC,则PM⊥AB,CM⊥AB,
所以∠PMC就是二面角PABC的平面角.在△PAB中,PM==1,同理MC=PC=1,则△PMC是等边三角形,所以∠PMC=60°.
答案:60°
4.已知平面α,β和直线m,l,则下列说法:
①若α⊥β,α∩β=m,l⊥m,则l⊥β;
②若α∩β=m,l⊂α,l⊥m,则l⊥β;
③若α⊥β,l⊂α,则l⊥β;
④若α⊥β,α∩β=m,l⊂α,l⊥m,则l⊥β.
其中正确的说法序号为 W.
解析:对于说法①缺少了条件:l⊂α;说法②缺少了条件:α⊥β;说法③缺少了条件:α∩β=m,l⊥m;说法④具备了面面垂直的性质定理的所有条件.
答案:④
5.如图,四边形ABCD,BD=2,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.求证:AB⊥DE.
证明:在△ABD中,因为AB=2,AD=4,BD=2,
所以AB2+BD2=AD2,所以AB⊥BD.
又因为平面EBD⊥平面ABD,
平面EBD∩平面ABD=BD,AB⊂平面ABD,
所以AB⊥平面EBD.
因为DE⊂平面EBD,所以AB⊥DE.
![]()
[A 基础达标]
1.经过平面α外一点和平面α内一点与平面α垂直的平面有 ( )
A.0个 B.1个
C.无数个 D.1个或无数个
解析:选D.当两点连线与平面α垂直时,可作无数个垂面,否则,只有1个.
2.从空间一点P向二面角αlβ的两个面α,β分别作垂线PE,PF,E,F为垂足,若∠EPF=60°,则二面角αlβ的平面角的大小是( )
A.60° B.120°
C.60°或120° D.不确定
解析:选C.若点P在二面角内,则二面角的平面角为120°;若点P在二面角外,则二面角的平面角为60°.
3.已知直线a,b与平面α,β,γ,下列能使α⊥β成立的条件是( )
A.α⊥γ,β⊥γ B.α∩β=a,b⊥a,b⊂β
C.a∥β,a∥α D.a∥α,a⊥β
解析:选D.由a∥α,知α内必有直线l与a平行.而a⊥β,所以l⊥β,所以α⊥β.
4.在四棱柱ABCDA1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC,AD=CD,则BD与CC1( )
A.平行 B.共面
C.垂直 D.不垂直
解析:选C.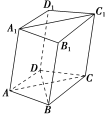 如图所示,在四边形ABCD中,因为AB=BC,AD=CD.
如图所示,在四边形ABCD中,因为AB=BC,AD=CD.
所以BD⊥AC.
因为平面AA1C1C⊥平面ABCD,平面AA1C1C∩平面ABCD=AC,
BD⊂平面ABCD,
所以BD⊥平面AA1C1C.
又CC1⊂平面AA1C1C,
所以BD⊥CC1,故选C.
5.如图,正四面体ABCD中,E,F分别是线段AC的三等分点,P是线段AB的中点,G是直线BD上的动点,则( )
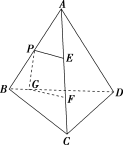
A.存在点G,使PG⊥EF成立
B.存在点G,使FG⊥EP成立
C.不存在点G,使平面EFG⊥平面ACD成立
D.不存在点G,使平面EFG⊥平面ABD成立
解析:选C.正四面体ABCD中,E,F分别是线段AC的三等分点,
P是线段AB的中点,G是直线BD上的动点,
在A中,不存在点G,使PG⊥EF成立,故A错误;
在B中,不存在点G,使FG⊥EP成立,故B错误;
在C中,不存在点G,使平面EFG⊥平面ACD成立,故C正确;
在D中,存在点G,使平面EFG⊥平面ABD成立,故D错误.故选C.
6.已知PA⊥矩形ABCD所在的平面(如图),则图中互相垂直的平面有 对.
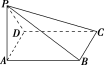
解析:因为DA⊥AB,DA⊥PA,所以DA⊥平面PAB,同理BC⊥平面PAB,又AB⊥平面PAD,所以DC⊥平面PAD,所以平面PAD⊥平面AC,平面PAB⊥平面AC,平面PBC⊥平面PAB,平面PAB⊥平面PAD,平面PDC⊥平面PAD,共5对.
答案:5
7.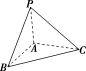 如图,在三棱锥PABC内,侧面PAC⊥底面ABC,且∠PAC=90°,PA=1,AB=2,则PB= W.
如图,在三棱锥PABC内,侧面PAC⊥底面ABC,且∠PAC=90°,PA=1,AB=2,则PB= W.
解析:因为侧面PAC⊥底面ABC,交线为AC,∠PAC=90°(即PA⊥AC),PA⊂平面PAC,
所以PA⊥平面ABC,
所以PA⊥AB,所以PB===.
答案:
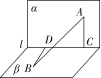 8.如图,直二面角αlβ,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,若AB=2,AC=BD=1,则CD的长为 W.
8.如图,直二面角αlβ,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,若AB=2,AC=BD=1,则CD的长为 W.
解析:如图,连接BC,
因为二面角αlβ为直二面角,AC⊂α,且AC⊥l,
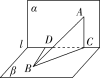 所以AC⊥β.
所以AC⊥β.
又BC⊂β,所以AC⊥BC,
所以BC2=AB2-AC2=3,
又BD⊥CD,
所以CD==.
答案:
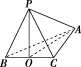
9.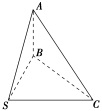 如图,过S点引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°.求证:平面ABC⊥平面BSC.
如图,过S点引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°.求证:平面ABC⊥平面BSC.
证明:取BC的中点D,连接SD、AD(图略),由SA=SB=SC,∠ASB=∠ASC=60°,得AB=AC=SA.
所以AD⊥BC,SD⊥BC,
所以∠ADS是二面角ABCS的平面角.
又∠BSC=90°,令SA=1,
则SD=2,AD=2,所以SD2+AD2=SA2.
所以∠ADS=90°,所以平面ABC⊥平面BSC.
10.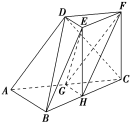 如图,三棱台DEFABC中, AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEFABC中, AB=2DE,G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
证明:
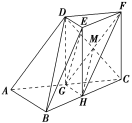 (1)如图所示,连接DG,设CD∩GF=M,连接MH.
(1)如图所示,连接DG,设CD∩GF=M,连接MH.
在三棱台DEFABC中,AB=2DE,所以AC=2DF.
因为G是AC的中点,
所以DF∥GC,且DF=GC,
所以四边形CFDG是平行四边形,所以DM=MC.因为BH=HC,所以MH∥BD.
又BD⊄平面FGH,MH⊂平面FGH,
所以BD∥平面FGH.
(2)因为G,H分别为AC,BC的中点,所以GH∥AB.
因为AB⊥BC,所以GH⊥BC.
又H为BC的中点,
所以EF∥HC,EF=HC,
所以四边形EFCH是平行四边形,所以CF∥HE.
因为CF⊥BC,所以HE⊥BC.
又HE,GH⊂平面EGH,HE∩GH=H,
所以BC⊥平面EGH.又BC⊂平面BCD,
所以平面BCD⊥平面EGH.
[B 能力提升]
11.将锐角A为60°,边长为a的菱形沿BD折成60°的二面角,则折叠后A与C之间的距离为( )
A.a B.2a
C.2a D.a
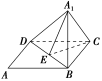 解析:选C.设折叠后点A到A1的位置,取BD的中点E,连接A1E,CE.
解析:选C.设折叠后点A到A1的位置,取BD的中点E,连接A1E,CE.
则BD⊥CE,BD⊥A1E.
于是∠A1EC为二面角A1BDC的平面角.
故∠A1EC=60°.
因为A1E=CE,所以△A1EC是等边三角形.
所以A1E=CE=A1C=2a.
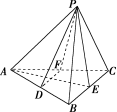 12.如图,在四面体PABC中,AB=AC,PB=PC,D,E,F分别是棱AB,BC,CA的中点,则下列结论中不一定成立的是( )
12.如图,在四面体PABC中,AB=AC,PB=PC,D,E,F分别是棱AB,BC,CA的中点,则下列结论中不一定成立的是( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面PAE
D.平面PDF⊥平面ABC
解析:选D.因为D,F分别为AB,AC的中点,则DF为△ABC的中位线,则BC∥DF,依据线面平行的判定定理,可知BC∥平面PDF,A成立.又E为BC的中点,且PB=PC,AB=AC,则BC⊥PE,BC⊥AE,依据线面垂直的判定定理,可知BC⊥平面PAE.因为BC∥DF,所以DF⊥平面PAE,B成立.又DF⊂平面PDF,则平面PDF⊥平面PAE,C成立.要使平面PDF⊥平面ABC,已知AE⊥DF,则必须有AE⊥PD或AE⊥PF,由条件知此垂直关系不一定成立,故选D.
13.如图所示,平面四边形ABCD,AB=AD=CD=1,BD=,BD⊥CD,将其沿对角线BD折成四面体ABCD,使平面ABD⊥平面BCD,则下列说法中正确的是( )
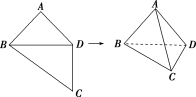
①平面ACD⊥平面ABD;②AB⊥CD;③平面ABC⊥平面ACD.
A.①② B.②③
C.①③ D.①②③
解析:选D.因为BD⊥CD,平面ABD⊥平面BCD,
所以CD⊥平面ABD,因为CD⊂平面ACD,
所以平面ACD⊥平面ABD,故①正确;
因为平面四边形ABCD中,
AB=AD=CD=1,BD=,
所以AB⊥AD,
又CD⊥平面ABD,所以AB⊥CD,
又AD∩CD=D,
所以AB⊥平面ACD,
又因为AB⊂平面ABC,
所以平面ABC⊥平面ACD,故②③正确.
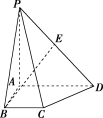 14.如图,在四棱锥PABCD中,底面ABCD是直角梯形,∠BAD=90°,AD∥BC,AB=BC=1,AD=2,PA⊥底面ABCD,PD与底面成45°角,点E是PD的中点.
14.如图,在四棱锥PABCD中,底面ABCD是直角梯形,∠BAD=90°,AD∥BC,AB=BC=1,AD=2,PA⊥底面ABCD,PD与底面成45°角,点E是PD的中点.
(1)求证:BE⊥PD;
(2)求二面角PCDA的余弦值.
解:(1)证明:连接AE.
因为PA⊥底面ABCD,所以∠PDA是PD与底面ABCD所成的角,
所以∠PDA=45°.所以PA=DA.
又因为点E是PD的中点,所以AE⊥PD.
因为PA⊥底面ABCD,AB⊂底面ABCD,
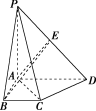 所以PA⊥AB.因为∠BAD=90°,所以BA⊥DA.
所以PA⊥AB.因为∠BAD=90°,所以BA⊥DA.
又因为PA∩AD=A,
所以BA⊥平面PDA.又因为PD⊂平面PDA,所以BA⊥PD.
又因为BA∩AE=A,
所以PD⊥平面ABE.
因为BE⊂平面ABE,
所以BE⊥PD.
(2)连接AC.在直角梯形ABCD中,
因为AB=BC=1,AD=2,
所以AC=CD=.因为AC2+CD2=AD2,
所以AC⊥CD,
又因为PA⊥底面ABCD,CD⊂底面ABCD,所以PA⊥CD.
因为AC∩PA=A,所以CD⊥平面PAC.
又因为PC⊂平面PAC,所以PC⊥CD,
所以∠PCA为二面角PCDA的平面角.
在Rt△PCA中,PC===.
所以cos∠PCA=PC=6=3.
所以所求二面角的余弦值为3.
[C 拓展探究]
15.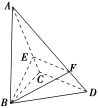 已知三棱锥ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且AC=AD=λ(0<λ<1).
已知三棱锥ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且AC=AD=λ(0<λ<1).
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD?
解:(1)证明:因为∠BCD=90°,所以BC⊥CD.
因为AB⊥平面BCD,所以AB⊥CD.
又因为AB∩BC=B,所以CD⊥平面ABC.
因为AC=AD,所以EF∥CD,
所以EF⊥平面ABC.
又因为EF⊂平面BEF,
所以平面BEF⊥平面ABC.
故不论λ为何值,总有平面BEF⊥平面ABC.
(2)由(1)得EF⊥平面ABC,BE⊂平面ABC,
所以EF⊥BE.
要使平面BEF⊥平面ACD,只需BE⊥AC.
因为∠BCD=90°,BC=CD=1,所以BD=.
又因为AB⊥平面BCD,∠ADB=60°,
所以AB=,AC=,
所以BE=AC=7,
所以AE=7,
所以λ=AC=7.
故当λ=7时,平面BEF⊥平面ACD.