![]() 8.3 简单几何体的表面积与体积
8.3 简单几何体的表面积与体积
第1课时 柱、锥、台的表面积和体积
![]()
考点 | 学习目标 | 核心素养 |
柱、锥、台的表面积 | 了解柱体、锥体、台体的侧面展开图,掌握柱体、柱、锥、台的体积 | 直观想象、数学运算 |
锥体、台体的表面积的求法 | 能利用柱体、锥体、台体的体积公式求体积,理解柱体、锥体、台体的体积之间的关系 | 直观想象、数学运算 |
![]()
![]() 问题导学
问题导学
预习教材P114-P117的内容,思考以下问题:
1.棱柱、棱锥、棱台的表面积如何计算?
2.圆柱、圆锥、圆台的侧面展开图分别是什么?
3.圆柱、圆锥、圆台的侧面积公式是什么?
4.柱体、锥体、台体的体积公式分别是什么?
5.圆柱、圆锥、圆台的侧面积公式、体积公式之间分别有怎样的关系?
![]()
1.棱柱、棱锥、棱台的表面积
多面体的表面积就是围成多面体各个面的面积的和.棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.
2.棱柱、棱锥、棱台的体积
(1)V棱柱=Sh;(2)V棱锥=3Sh;V棱台=3h(S′++S),其中S′,S分别是棱台的上、下底面面积,h为棱台的高.
3.圆柱、圆锥、圆台的表面积和体积
名称 | 图形 | 公式 |
圆柱 |
| 底面积:S底=πr2 侧面积:S侧=2πrl 表面积:S=2πrl+2πr2 体积:V=πr2l |
圆锥 |
| 底面积:S底=πr2 侧面积:S侧=πrl 表面积:S=πrl+πr2 体积:V=3πr2h |
圆台 |
| 上底面面积:S上底=πr′2 下底面面积:S下底=πr2 侧面积:S侧=πl(r+r′) 表面积: S=π(r′2+r2+r′l+rl) 体积: V=3πh(r′2+r′r+r2) |
■名师点拨
1.柱体、锥体、台体的体积
(1)柱体:柱体的底面面积为S,高为h,则V=Sh.
(2)锥体:锥体的底面面积为S,高为h,则V=3Sh.
(3)台体:台体的上、下底面面积分别为S′、S,高为h,则V=3h.
2.圆柱、圆锥、圆台的侧面积公式之间的关系
S圆柱侧=2πrlr′=rS圆台侧=π(r′+r)lr′=0S圆锥侧=πrl.
3.柱体、锥体、台体的体积公式之间的关系
V柱体=ShS′=SV台体=3(S′++S)hS′=0V锥体=3Sh.
![]()
![]() 判断(正确的打“√”,错误的打“×”)
判断(正确的打“√”,错误的打“×”)
(1)几何体的表面积就是其侧面面积与底面面积的和.( )
(2)几何体的侧面积是指各个侧面的面积之和.( )
(3)等底面面积且等高的两个同类几何体的体积相同.( )
(4)在三棱锥PABC中,VPABC=VAPBC=VBPAC=VCPAB.( )
答案:(1)√ (2)√ (3)√ (4)√
![]() 棱长都是 1 的三棱锥的表面积为( )
棱长都是 1 的三棱锥的表面积为( )
A. B.2 C.3 D.4
解析:选 A.S表=4S正△=4×4=.
![]() 若长方体的长、宽、高分别为 3 cm,4 cm,5 cm,则长方体的体积为( )
若长方体的长、宽、高分别为 3 cm,4 cm,5 cm,则长方体的体积为( )
A.27 cm3 B.60 cm3 C.64 cm3 D.125 cm3
解析:选 B.长方体即为四棱柱,其体积为底面积×高,即为 3×4×5=60(cm3).
![]() 圆台的上、下底面半径分别为 3 和 4,母线长为 6,则其表面积等于( )
圆台的上、下底面半径分别为 3 和 4,母线长为 6,则其表面积等于( )
A.72 B.42π C.67π D.72π
解析:选 C.S表=π(32+42+3×6+4×6)=67π.
![]()
![]()
柱、锥、台的表面积
![]() (1)若圆锥的正视图是正三角形,则它的侧面积是底面积的( )
(1)若圆锥的正视图是正三角形,则它的侧面积是底面积的( )
A.倍 B.3 倍
C.2 倍 D.5 倍
(2)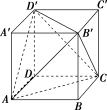 已知正方体的 8 个顶点中,有 4 个为侧面是等边三角形的三棱锥的顶点,则这个三棱锥与正方体的表面积之比为( )
已知正方体的 8 个顶点中,有 4 个为侧面是等边三角形的三棱锥的顶点,则这个三棱锥与正方体的表面积之比为( )
A.1∶ B.1∶
C.2∶ D.3∶
(3)已知某圆台的一个底面周长是另一个底面周长的 3 倍,母线长为 3 ,圆台的侧面积为 84π,则该圆台较小底面的半径为( )
A.7 B.6
C.5 D.3
【解析】 (1)设圆锥的底面半径为 r,母线长为 l,则由题意可知,l=2r,于是 S侧=πr·2r=2πr2,S底=πr2,可知选 C.
(2)棱锥 B′ACD′为适合条件的棱锥,四个面为全等的等边三角形,设正方体的棱长为 1,则 B′C=,S△B′AC=2.
三棱锥的表面积 S锥=4×2=2,
又正方体的表面积 S正=6.
因此 S锥∶S正=2∶6=1∶.
(3)设圆台较小底面的半径为 r,则另一底面的半径为 3r.由 S侧=3π(r+3r)=84π,解得 r=7.
【答案】 (1)C (2)B (3)A
![]()
空间几何体表面积的求法技巧
(1)多面体的表面积是各个面的面积之和.
(2)组合体的表面积应注意重合部分的处理.
(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开为平面图形计算,而表面积是侧面积与底面圆的面积之和.
![]() 已知正四棱台(正四棱锥被平行于底面的平面所截,截面与底面间的部分)上底面边长为4,侧棱和下底面边长都是8,求它的侧面面积.
已知正四棱台(正四棱锥被平行于底面的平面所截,截面与底面间的部分)上底面边长为4,侧棱和下底面边长都是8,求它的侧面面积.
解:法一:设正四棱台为ABCDA1B1C1D1,如图①.设B1F为斜高.
在Rt△B1FB中,BF=2×(8-4)=2,B1B=8,
所以B1F= =2,
所以S正棱台侧=4×2×(4+8)×2
=48.
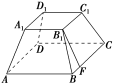
①
法二: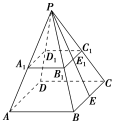 设正四棱台为ABCDA1B1C1D1,延长正四棱台的侧棱交于点P,作面PBC上的斜高PE,交B1C1于E1,如图②.
设正四棱台为ABCDA1B1C1D1,延长正四棱台的侧棱交于点P,作面PBC上的斜高PE,交B1C1于E1,如图②.
设PB1=x,则x+8=8,
解得x=8.
所以PB1=B1B=8,
所以E1为PE的中点,
又PE1=111= =2, ②
所以PE=2PE1=4.
所以S正棱台侧=S大正棱锥侧-S小正棱锥侧
=4×2×8×PE-4×2×4×PE1
=4×2×8×4-4×2×4×2
=48.
![]()
柱、锥、台的体积
![]() 如图所示,正方体ABCDA1B1C1D1的棱长为a,过顶点B,D,A1截下一个三棱锥.
如图所示,正方体ABCDA1B1C1D1的棱长为a,过顶点B,D,A1截下一个三棱锥.
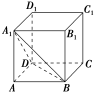
(1)求剩余部分的体积;
(2)求三棱锥AA1BD的体积及高.
【解】 (1)V三棱锥A1ABD=3S△ABD·A1A
=3×2·AB·AD·A1A=6a3.
故剩余部分的体积
V=V正方体-V三棱锥A1ABD=a3-6a3=6a3.
(2)V三棱锥AA1BD=V三棱锥A1ABD=6a3.
设三棱锥AA1BD的高为h,
则V三棱锥AA1BD=3·S△A1BD·h
=3×2×2(a)2h=6a2h,
故6a2h=6a3,
解得h=3a.
![]()
求几何体体积的常用方法
(1)公式法:直接代入公式求解.
(2)等积法:例如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可.
(3)补体法:将几何体补成易求解的几何体,如棱锥补成棱柱,棱台补成棱锥等.
(4)分割法:将几何体分割成易求解的几部分,分别求体积.
[提醒] 求几何体的体积时,要注意利用好几何体的轴截面(尤其为圆柱、圆锥时),准确求出几何体的高和底面积.
![]()
1.圆锥的轴截面是等腰直角三角形,侧面积是 16π,则圆锥的体积是( )
A.3 B.3
C.64π D.128π
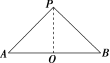 解析:选 A.作圆锥的轴截面,如图所示.由题设,在 △PAB中,∠APB=90°,PA=PB.
解析:选 A.作圆锥的轴截面,如图所示.由题设,在 △PAB中,∠APB=90°,PA=PB.
设圆锥的高为 h,底面半径为 r,
则 h=r,PB=r.
由 S侧=π·r·PB=16π,
得πr2=16π.所以 r=4.则 h=4.
故圆锥的体积 V圆锥=3πr2h=3π.
2.圆柱的侧面展开图是长 12 cm,宽 8 cm 的矩形,则这个圆柱的体积为( )
A.π cm3 B.π cm3
C.π cm3或π cm3 D.192π cm3
解析:选 C.当圆柱的高为 8 cm时, V=π×2π×8=π(cm3),当圆柱的高为 12 cm时,V=π×2π×12=π(cm3).
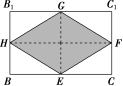
3.(2019·高考全国卷Ⅲ)学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCDA1B1C1D1挖去四棱锥OEFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为________g.
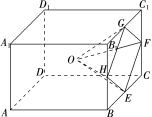
解析:由题易得长方体ABCDA1B1C1D1的体积为6×6×4=144(cm3),四边形EFGH为平行四边形,如图所示,连接GE,HF,易知四边形EFGH的面积为矩形BCC1B1面积的一半,即2×6×4=12(cm2),所以V四棱锥OEFGH=3×3×12=12(cm3),所以该模型的体积为144-12=132(cm3),所以制作该模型所需原料的质量为132×0.9=118.8(g).
答案:118.8
![]()
组合体的表面积和体积
![]() 如图在底面半径为 2,母线长为 4 的圆锥中内接一个高为的圆柱,求圆柱的表面积.
如图在底面半径为 2,母线长为 4 的圆锥中内接一个高为的圆柱,求圆柱的表面积.
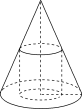
【解】 设圆锥的底面半径为 R,圆柱的底面半径为 r,表面积为 S.
则 R=OC=2,AC=4,
AO==2.
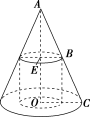 如图所示,
如图所示,
易知△AEB∽△AOC,
所以AO=OC,即3=2,所以 r=1,
S底=2πr2=2π,S侧=2πr·h=2π.
所以 S=S底+S侧=2π+2π
=(2+2)π.
![]()
1.[变问法]本例中的条件不变,求圆柱的体积与圆锥的体积之比.
解:由例题解析可知:圆柱的底面半径为 r=1,高 h=,所以圆柱的体积 V1=πr2h=π×12×=π.
圆锥的体积 V2=3π×22×2=3π.
所以圆柱与圆锥的体积比为 3∶8.
2.[变问法]本例中的条件不变,求图中圆台的表面积与体积.
解:由例题解析可知:圆台的上底面半径 r=1,下底面半径 R=2,高 h=,母线 l=2,所以圆台的表面积 S=π(r2+R2+r·l+Rl)=π(12+22+1×2+2×2)=11π.
圆台的体积 V=3π(r2+rR+R2)h=3π(12+2+22)×=3π.
3.[变条件、变问法]本例中的“高为”改为“高为 h”,试求圆柱侧面积的最大值.
解:设圆锥的底面半径为 R,圆柱的底面半径为 r,
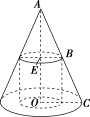 则 R=OC=2,AC=4,
则 R=OC=2,AC=4,
AO==2.
如图所示易知△AEB∽△AOC,
所以AO=OC,
即3=2,
所以 h=2-r,
S圆柱侧=2πrh=2πr(2-r)
=-2πr2+4πr,
所以当 r=1,h=时,圆柱的侧面积最大,其最大值为 2π.
![]()
求组合体的表面积与体积的步骤
(1)分析结构特征:弄清组合体的组成形式,找准有关简单几何体的关键量.
(2)设计计算方法:根据组成形式,设计计算方法,特别要注意“拼接面”面积的处理,利用“切割”“补形”的方法求体积.
(3)计算求值:根据设计的计算方法求值.
![]()
1.如图,在多面体 ABCDEF 中,已知面 ABCD 是边长为 4 的正方形,EF∥AB,EF=2,EF 上任意一点到平面 ABCD 的距离均为 3,求该多面体的体积.
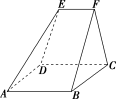
解:如图,连接 EB,EC.四棱锥 EABCD 的体积
V四棱锥 EABCD=3×42×3=16.
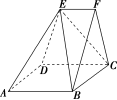 因为AB=2EF,EF∥AB,所以S△EAB=2S△BEF.所以V三棱锥 FEBC
因为AB=2EF,EF∥AB,所以S△EAB=2S△BEF.所以V三棱锥 FEBC
=V三棱锥 CEFB=2V三棱锥 CABE
=2V三棱锥 EABC=2×2V四棱锥 EABCD=4.
所以多面体的体积 V=V四棱锥 EABCD+V三棱锥 FEBC=16+4=20.
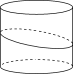
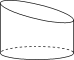 2.如图,一个底面半径为 2 的圆柱被一平面所截,截得的几何体的最短和最长母线长分别为 2 和 3,求该几何体的体积.
2.如图,一个底面半径为 2 的圆柱被一平面所截,截得的几何体的最短和最长母线长分别为 2 和 3,求该几何体的体积.
解:用一个完全相同的几何体把题中几何体补成一个圆柱,如图,则圆柱的体积为 π×22×5=20π,故所求几何体的体积为 10π.
![]()
1.已知某长方体同一顶点上的三条棱长分别为1,2,3,则该长方体的表面积为( )
A.22 B.20
C.10 D.11
解析:选A.所求长方体的表面积S=2×(1×2)+2×(1×3)+2×(2×3)=22.
2.正三棱锥的高为3,侧棱长为2,则这个正三棱锥的体积为( )
A.4 B.4
C.4 D.4
解析:选D.由题意可得底面正三角形的边长为3,所以V=3×4×32×3=4.故选D.
3.已知圆台的上、下底面的面积之比为9∶25,那么它的中截面截得的上、下两台体的侧面积之比是________.
解析:圆台的上、下底面半径之比为3∶5,设上、下底面半径为3x,5x,则中截面半径为4x,设上台体的母线长为l,
则下台体的母线长也为l,上台体侧面积S1=π(3x+4x)l=7πxl,下台体侧面积S2=π(4x+5x)l=9πxl,所以S1∶S2=7∶9.
答案:7∶9
4.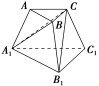 如图,三棱台ABCA1B1C1中,AB∶A1B1=1∶2,求三棱锥A1ABC,三棱锥BA1B1C,三棱锥CA1B1C1的体积之比.
如图,三棱台ABCA1B1C1中,AB∶A1B1=1∶2,求三棱锥A1ABC,三棱锥BA1B1C,三棱锥CA1B1C1的体积之比.
解:设棱台的高为h,S△ABC=S,则S△A1B1C1=4S.
所以VA1ABC=3S△ABC·h=3Sh,
VCA1B1C1=3S△A1B1C1·h=3Sh.
又V台=3h(S+4S+2S)=3Sh,
所以VBA1B1C=V台-VA1ABC-VCA1B1C1
=3Sh-3-3=3Sh,
所以体积比为1∶2∶4.
![]()
[A 基础达标]
1.若某圆锥的高等于其底面直径,则它的底面积与侧面积之比为( )
A.1∶2 B.1∶
C.1∶ D.∶2
解析:选C.设圆锥底面半径为r,则高h=2r,所以其母线长l=r.所以S侧=πrl=πr2,S底=πr2,S底∶S侧=1∶.
2.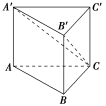 如图,ABCA′B′C′是体积为1的棱柱,则四棱锥CAA′B′B的体积是( )
如图,ABCA′B′C′是体积为1的棱柱,则四棱锥CAA′B′B的体积是( )
A.3 B.2
C.3 D.4
解析:选C.因为VCA′B′C′
=3VABCA′B′C′=3,
所以VCAA′B′B=1-3=3.
3.(2018·高考全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.12π B.12π
C.8π D.10π
解析:选B.设所截正方形的边长为 a,则 a2=8,即 a=2.所以圆柱的母线长为 2,底面圆半径 r=,所以圆柱的表面积为 2π×2+π()2×2=8π+4π=12π.
4.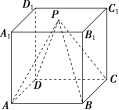 如图,正方体ABCDA1B1C1D1的棱长为1,点P是面A1B1C1D1内任意一点,则四棱锥PABCD的体积为( )
如图,正方体ABCDA1B1C1D1的棱长为1,点P是面A1B1C1D1内任意一点,则四棱锥PABCD的体积为( )
A.6 B.3
C.2 D.3
解析:选B.因为正方体ABCDA1B1C1D1的棱长为1,
点P是面A1B1C1D1内任意一点,
所以点P到平面ABCD的距离d=AA1=1,
S正方形ABCD=1×1=1,
所以四棱锥PABCD的体积为:
VPABCD=3×AA1×S正方形ABCD=3×1×1=3.
故选B.
5.(2019·临川检测)一个封闭的正三棱柱容器,高为 3,内装水若干(如图甲,底面处于水平状态),将容器放倒(如图乙,一个侧面处于水平状态),这时水面与各棱交点 E,F,F1,E1 分别为所在棱的中点,则图甲中水面的高度为( )
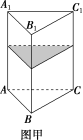
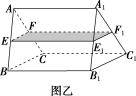
A.2 B.4
C.2 D.4
解析:选 D.因为 E,F,F1,E1 分别为所在棱的中点,所以棱柱 EFCBE1F1C1B1 的体积 V=S梯形EFCB×3=4S△ABC×3=4S△ABC.设甲中水面的高度为 h,则 S△ABC×h=4S△ABC,解得h=4,故选 D.
6.已知圆柱 OO′的母线 l=4 cm,表面积为 42π cm2,则圆柱 OO′的底面半径 r=______cm.
解析:圆柱 OO′的侧面积为 2πrl=8πr(cm2),两底面面积为 2×πr2=2πr2(cm2),
所以 2πr2+8πr=42π,
解得 r=3 或 r=-7(舍去),
所以圆柱的底面半径为 3 cm.
答案:3
7.表面积为 3π的圆锥,它的侧面展开图是一个半圆面,则该圆锥的底面直径为________.
解析:设圆锥的母线为 l,圆锥底面半径为 r,由题意可知,πrl+πr2=3π,且 πl=2πr.解得 r=1,即直径为 2.
答案:2
8.圆柱内有一个内接长方体 ABCDA1B1C1D1,长方体的体对角线长是 10 cm,圆柱的侧面展开图为矩形,此矩形的面积是 100π cm 2,则圆柱的底面半径为______cm,高为______cm.
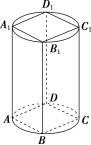
解析:设圆柱底面半径为 r cm,高为 h cm,如图所示,则圆柱轴截面长方形的对角线长等于它的内接长方体的体对角线长,则:
2πrh=100π,
所以h=10.
即圆柱的底面半径为 5 cm,高为 10 cm.
答案:5 10
9.如图,已知正三棱锥 SABC 的侧面积是底面积的 2 倍,正三棱锥的高 SO=3,求此正三棱锥的表面积.
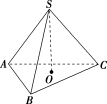
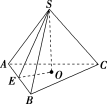 解:如图,设正三棱锥的底面边长为 a,斜高为 h′,过点 O 作 OE⊥AB,与 AB 交于点 E,连接 SE,则 SE⊥AB,
解:如图,设正三棱锥的底面边长为 a,斜高为 h′,过点 O 作 OE⊥AB,与 AB 交于点 E,连接 SE,则 SE⊥AB,
SE=h′.
因为 S侧=2S底,
所以 3×2·a·h′=4a2×2.
所以 a=h′.
因为 SO⊥OE,
所以 SO2+OE2=SE2.
所以 32+h′=h′2.
所以 h′=2,所以 a=h′=6.
所以 S底=4a2=4×62=9,
S侧=2S底=18.
所以 S表=S侧+S底=18+9=27.
10.若 E,F 是三棱柱 ABCA1B1C1 侧棱 BB1和 CC1 上的点,且 B1E =CF,三棱柱的体积为 m,求四棱锥 ABEFC 的体积.
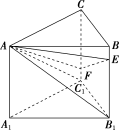 解:如图所示,
解:如图所示,
连接 AB1,AC1.
因为 B1E =CF,
所以 梯形 BEFC 的面积等于梯形 B1EFC1 的面积.
又四棱锥 ABEFC 的高与四棱锥 AB1EFC1 的高相等,
所以 V ABEFC=VAB1EFC1
=2VABB1C1C.
又 VA A1B1C1=3S△A1B1C1·h,
VABCA1B1C1=S△A1B1C1·h=m,所以
VAA1B1C1=3,
所以 VABB1C1C=VABCA1B1C1-VAA1B1C1=3m.
所以 VABEFC=2×3m=3,
即四棱锥 ABEFC 的体积是3.
[B 能力提升]
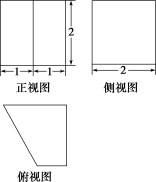
11.(2018·高考浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A.2 B.4
C.6 D.8
解析:选 C.由三视图可知,该几何体是一个底面为直角梯形的直四棱柱,所以该几何体的体积 V=2×(1+2)×2×2=6.故选 C.
12.(2019·高考全国卷Ⅱ)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1,则该半正多面体共有________个面,其棱长为________.
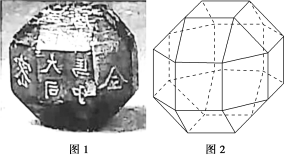
解析:依题意知,题中的半正多面体的上、下、左、右、前、后6个面都在正方体的表面上,且该半正多面体的表面由18个正方形,8个正三角形组成,因此题中的半正多面体共有26个面.注意到该半正多面体的俯视图的轮廓是一个正八边形,设题中的半正多面体的棱长为x,则2x+x+2x=1,解得x=-1,故题中的半正多面体的棱长为-1.
答案:26 -1
13.用一张正方形的纸把一个棱长为 1 的正方体礼品盒完全包住,不将纸撕开,则所需纸的最小面积是________.
解析:如图①为棱长为 1 的正方体礼品盒,先把正方体的表面按图所示方式展开成平面图形,再把平面图形尽可能拼成面积较小的正方形,如图②所示,由图知正方形的边长为 2,其面积为 8.
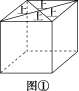
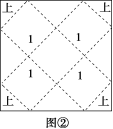
答案:8
14.如图所示,已知三棱柱ABCA′B′C′,侧面B′BCC′的面积是S,点A′到侧面B′BCC′的距离是a,求证:三棱柱ABCA′B′C′的体积V=2Sa.
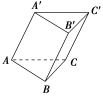
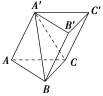 证明:法一:如图所示,连接A′B,A′C,这样就把三棱柱分割成了两个棱锥.
证明:法一:如图所示,连接A′B,A′C,这样就把三棱柱分割成了两个棱锥.
显然三棱锥A′ABC的体积是3V,而四棱锥A′BCC′B′的体积为3Sa,故有3V+3Sa=V,
所以三棱柱ABCA′B′C′的体积V=2Sa.
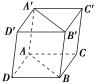 法二:如图所示,将三棱柱ABCA′B′C′补成一个四棱柱ACBDA′C′B′D′,其中AC∥BD,AD∥BC,即ACBD为一个平行四边形,显然三棱柱ABDA′B′D′的体积与原三棱柱ABCA′B′C′的体积相等.
法二:如图所示,将三棱柱ABCA′B′C′补成一个四棱柱ACBDA′C′B′D′,其中AC∥BD,AD∥BC,即ACBD为一个平行四边形,显然三棱柱ABDA′B′D′的体积与原三棱柱ABCA′B′C′的体积相等.
因为四棱柱ACBDA′C′B′D′以BCC′B′为底面,高为点A′到面BCC′B′的距离,所以补形后的四棱柱的体积为Sa,于是三棱柱ABCA′B′C′的体积V=2Sa.
[C 拓展探究]
15.某养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪用).已建的仓库的底面直径为12 m,高为4 m.养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪种方案更经济些?
解:(1)设两种方案所建的仓库的体积分别为V1,V2.
方案一:仓库的底面直径变成16 m,则其体积V1=3×π×2×4=3π(m3);
方案二:仓库的高变成8 m,则其体积V2=3×π×2×8=96π(m3).
(2)设两种方案所建的仓库的表面积分别为S1,S2.
方案一:仓库的底面直径变成16 m,半径为8 m,
此时圆锥的母线长为l1==4(m),
则仓库的表面积S1=π×8×(8+4)
=(64+32)π(m2);
方案二:仓库的高变成8 m,此时圆锥的母线长为l2==10(m),
则仓库的表面积S2=π×6×(6+10)
=96π(m2).
(3)因为V2>V1,S2<S1,
所以方案二比方案一更加经济.