![]() 6.4 平面向量的应用
6.4 平面向量的应用
6.4.1 平面几何中的向量方法
6.4.2 向量在物理中的应用举例
![]()
考点 | 学习目标 | 核心素养 |
向量在平面几何中的应用 | 会用向量方法解决平面几何中的平行、 垂直、长度、夹角等问题 | 数学建模、逻辑推理 |
向量在物理中的应用 | 会用向量方法解决物理中的速度、力学问题 | 数学建模、数学运算 |
![]()
![]() 问题导学
问题导学
预习教材P38-P41的内容,思考以下问题:
1.利用向量可以解决哪些常见的几何问题?
2.如何用向量方法解决物理问题?
![]()
1.用向量方法解决平面几何问题的“三个步骤”

2.向量在物理学中的应用
(1)由于物理学中的力、速度、位移都是矢量,它们的分解与合成与向量的减法和加法相似,可以用向量的知识来解决.
(2)物理学中的功是一个标量,即为力F与位移s的数量积,即W=F·s=|F||s|cos θ(θ为F与s的夹角).
![]()
![]() 判断(正确的打“√”,错误的打“×”)
判断(正确的打“√”,错误的打“×”)
(1)求力F1和F2的合力可按照向量加法的平行四边形法则. ( )
(2)若△ABC为直角三角形,则有→·→=0.( )
(3)若向量→∥→,则AB∥CD.( )
答案:(1)√ (2)× (3)×
![]() 若向量→=(2,2),→=(-2,3)分别表示两个力F1,F2,则|F1+F2|为( )
若向量→=(2,2),→=(-2,3)分别表示两个力F1,F2,则|F1+F2|为( )
A.(0,5) B.(4,-1)
C.2 D.5
解析:选D.F1+F2=(2,2)+(-2,3)=(0,5),所以|F1+F2|=5.
![]() 力F=(-1,-2)作用于质点P,使P产生的位移为s=(3,4),则力F对质点P做的功是________.
力F=(-1,-2)作用于质点P,使P产生的位移为s=(3,4),则力F对质点P做的功是________.
解析:因为W=F·s=(-1,-2)·(3,4)=-11,则力F对质点P做的功是-11.
答案:-11
![]() 若→=3e,→=5e,且|→|=|→|,则四边形ABCD的形状为________.
若→=3e,→=5e,且|→|=|→|,则四边形ABCD的形状为________.
解析:由→=3e,→=5e,得→∥→,→≠→,又因为ABCD为四边形,所以AB∥DC,AB≠DC.
又|→|=|→|,得AD=BC,
所以四边形ABCD为等腰梯形.
答案:等腰梯形
![]()
![]()
向量在几何中的应用
角度一 平面几何中的垂直问题
![]()
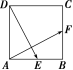 如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
证明:法一:设→=a,→=b,
则|a|=|b|,a·b=0,
又→=→+→=-a+2b,→=→+→=b+2a,
所以→·→=a·b=-2a2-4a·b+2b2=-2|a|2+2|b|2=0.
故→⊥→,即AF⊥DE.
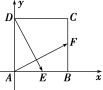 法二:如图,建立平面直角坐标系,设正方形的边长为2,则A(0,0),D(0,2),E(1,0),F(2,1),→=(2,1),→=(1,-2).
法二:如图,建立平面直角坐标系,设正方形的边长为2,则A(0,0),D(0,2),E(1,0),F(2,1),→=(2,1),→=(1,-2).
因为→·→=(2,1)·(1,-2)=2-2=0,
所以→⊥→,即AF⊥DE.
角度二 平面几何中的平行(或共线)问题
![]()
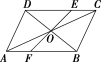 如图,点O是平行四边形ABCD的中心,E,F分别在边CD,AB上,且ED=FB=2.求证:点E,O,F在同一直线上.
如图,点O是平行四边形ABCD的中心,E,F分别在边CD,AB上,且ED=FB=2.求证:点E,O,F在同一直线上.
证明:设→=m,→=n,
由ED=FB=2,知E,F分别是CD,AB的三等分点,
所以→=→+→=3→+2→
=-3m+2(m+n)=6m+2n,
→=→+→=2→+3→
=2(m+n)-3m=6m+2n.
所以→=→.
又O为→和→的公共点,故点E,O,F在同一直线上.
角度三 平面几何中的长度问题
![]()
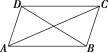 如图,平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2,求对角线AC的长.
如图,平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2,求对角线AC的长.
解:设→=a,→=b,则→=a-b,→=a+b,
而|→|=|a-b|====2,
所以5-2a·b=4,所以a·b=2,又|→|2=|a+b|2=a2+2a·b+b2=1+4+2a·b=6,所以|→|=,即AC=.
![]()
用向量方法解决平面几何问题的步骤

![]() 已知A,B,C,D四点的坐标分别为(1,0),(4,3),(2,4),(0,2),则此四边形为( )
已知A,B,C,D四点的坐标分别为(1,0),(4,3),(2,4),(0,2),则此四边形为( )
A.梯形 B.菱形
C.矩形 D.正方形
解析:选A.→=(3,3),→=(-2,-2),所以→=-2→,→与→共线,但|→|≠|→|,故此四边形为梯形.
![]()
向量在物理中的应用
![]() (1)在长江南岸某渡口处,江水以12.5 km/h的速度向东流,渡船的速度为25 km/h.渡船要垂直地渡过长江,其航向应如何确定?
(1)在长江南岸某渡口处,江水以12.5 km/h的速度向东流,渡船的速度为25 km/h.渡船要垂直地渡过长江,其航向应如何确定?
(2)已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0),求F1,F2分别对质点所做的功.
【解】 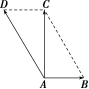 (1)如图,设→表示水流的速度,→表示渡船的速度,→表示渡船实际垂直过江的速度.
(1)如图,设→表示水流的速度,→表示渡船的速度,→表示渡船实际垂直过江的速度.
因为→+→=→,所以四边形ABCD为平行四边形.
在Rt△ACD中,∠ACD=90°,|→|=|→|=12.5.
|→|=25,所以∠CAD=30°,即渡船要垂直地渡过长江,其航向应为北偏西30°.
(2)设物体在力F作用下的位移为s,则所做的功为W=F·s.
因为→=(7,0)-(20,15)=(-13,-15).
所以W1=F1·→=(3,4)·(-13,-15)
=3×(-13)+4×(-15)=-99(焦),
W2=F2·→=(6,-5)·(-13,-15)
=6×(-13)+(-5)×(-15)=-3(焦).
![]()
用向量方法解决物理问题的“三步曲”

![]() 已知两个力F1,F2的夹角为90°,它们的合力大小为10 N,合力与F1的夹角为60°,那么F1的大小为( )
已知两个力F1,F2的夹角为90°,它们的合力大小为10 N,合力与F1的夹角为60°,那么F1的大小为( )
A.5 N B.5 N
C.10 N D.5 N
解析:选B.画出图形,如图,由题意|F1+F2|=10 N,所以|F1|=|F1+F2|cos 60°=5 N,故选B.

![]()
1.河水的流速为2 m/s,一艘小船以垂直于河岸方向10 m/s的速度驶向对岸,则小船在静水中的速度大小为( )
A.10 m/s B.2 m/s
C.4 m/s D.12 m/s
解析:选B.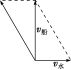 由题意知|v水|=2 m/s,|v船|=10 m/s,作出示意图如图.
由题意知|v水|=2 m/s,|v船|=10 m/s,作出示意图如图.
所以小船在静水中的速度大小
|v|==2(m/s).
2.已知三个力f1=(-2,-1),f2=(-3,2),f3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,再加上一个力f4,则f4=( )
A.(-1,-2) B.(1,-2)
C.(-1,2) D.(1,2)
解析:选D.由物理知识知f1+f2+f3+f4=0,故f4=-(f1+f2+f3)=(1,2).
3.设P,Q分别是梯形ABCD的对角线AC与BD的中点,AB∥DC,试用向量证明:PQ∥AB.
证明:设→=λ→(λ>0且λ≠1),因为→=→-→=→+→-→=→+2(→-→)
=→+2[(→-→)-(→+→)]
=→+2(→-→)
=2(→+→)=2(-λ+1)→,
所以→∥→,又P,Q,A,B四点不共线,所以PQ∥AB.
![]() [A 基础达标]
[A 基础达标]
1.已知平面内四边形ABCD和点O,若→=a,→=b,→=c,→=d,且a+c=b+d,则四边形ABCD为( )
A.菱形 B.梯形
C.矩形 D.平行四边形
解析:选D.由题意知a-b=d-c,所以→=→,所以四边形ABCD为平行四边形.故选D.
2.如果一架飞机先向东飞行200 km,再向南飞行300 km,设飞机飞行的路程为s km,位移为a,则( )
A.s>|a|
B.s<|a|
C.s=|a|
D.s与|a|不能比较大小
解析:选A.物理量中的路程是数量,位移是向量,从而s=500,由位移的合成易得|a|<500,故s>|a|.
3.一质点受到平面上的三个力F1,F2,F3的作用而处于平衡状态.已知F1与F2的夹角为60°,且F1,F2的大小分别为2 N和4 N,则F3的大小为( )
A.6 N B.2 N
C.2 N D.2 N
解析:选D.由向量的平行四边形法则及力的平衡,得|F3|2=|-F1-F2|2=|F1|2+|F2|2+2|F1|·|F2|·cos 60°=22+42+2×2×4×2=28,所以|F3|=2 N.
4.在△ABC中,AB=3,AC边上的中线BD=,→·→=5,则AC的长为( )
A.1 B.2
C.3 D.4
解析:选B.因为→=→-→=2→-→,
所以→2=→=4→2-→·→+→2,
即4→2=1,所以|→|=2,即AC=2.
5.在△ABC中,有下列四个命题:
①→-→=→;
②→+→+→=0;
③若(→+→)·(→-→)=0,则△ABC为等腰三角形;
④若→·→>0,则△ABC为锐角三角形.
其中正确的命题有( )
A.①② B.①④
C.②③ D.②③④
解析:选C.因为→-→=→=-→≠→,所以①错误.→+→+→=→+→=→-→=0,所以②正确.由(→+→)·(→-→)=→2-→2=0,得|→|=|→|,所以△ABC为等腰三角形,③正确.→·→>0⇒cos A>0,所以A为锐角,但不能确定B,C的大小,所以不能判定△ABC是否为锐角三角形,所以④错误.故选C.
6.用两条成120°角的等长绳子悬挂一个灯具,已知灯具重量为10 N,则每根绳子的拉力大小为______N.
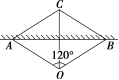
解析:如图,由题意,得∠AOC=∠COB=60°,|→|=10,
则|→|=|→|=10,即每根绳子的拉力大小为10 N.
答案:10
7.点P在平面上做匀速直线运动,速度v=(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|v|个单位).设开始时点P0的坐标为(-10,10),则5秒后点P的坐标为________.
解析:由题意知,→=5v=(20,-15),
设点P的坐标为(x,y),则y-10=-15,
解得点P的坐标为(10,-5).
答案:(10,-5)
8.在矩形ABCD中,AB=2,AD=1.边DC上的动点P(包含点D,C)与CB延长线上的动点Q(包含点B)满足|→|=|→|,则→·→的最小值为________.
解析: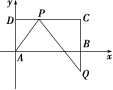 以点A为坐标原点,分别以AB,AD所在直线为x轴,y轴建立如图所示的平面直角坐标系,
以点A为坐标原点,分别以AB,AD所在直线为x轴,y轴建立如图所示的平面直角坐标系,
设P(x,1),Q(2,y),由题意知0≤x≤2,-2≤y≤0.
因为|→|=|→|,所以|x|=|y|,所以x=-y.
因为→=(-x,-1),→=(2-x,y-1),
所以→·→=-x(2-x)-(y-1)
=x2-2x-y+1
=x2-x+1
=2+4,
所以当x=2时,→·→取得最小值,为4.
答案:4
9.已知△ABC是直角三角形,CA=CB,D是CB的中点,E是AB上的一点,且AE=2EB.求证:AD⊥CE.
证明:以C为原点,→方向为x轴正方向,建立平面直角坐标系.
设AC=a,则A(a,0),B(0,a),
D2,C(0,0),Ea.
因为→=2,→=a.
所以→·→=-a·3a+2·3a=0,所以→⊥→,即AD⊥CE.
10.如图,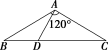 在△ABC中,∠BAC=120°,AB=AC=3,点D在线段BC上,且BD=2DC.求:
在△ABC中,∠BAC=120°,AB=AC=3,点D在线段BC上,且BD=2DC.求:
(1)AD的长;
(2)∠DAC的大小.
【解】 (1)设→=a,→=b,
则→=→+→=→+3→=→+3(→-→)
=3→+3→=3a+3b.
所以|→|2=→2=b=9a2+2·9a·b+9b2=9×9+2×9×3×3×cos 120°+9×9=3.
故AD=.
(2)设∠DAC=θ,则θ为向量→与→的夹角.
因为cos θ=|=×3=3=3=0,
所以θ=90°,即∠DAC=90°.
[B 能力提升]
11.在▱ABCD中,AD=1,∠BAD=60°,E为CD的中点,若→·→=1,则AB的长为( )
A.1 B.2
C.3 D.2
解析:选B.设AB的长为a(a>0),
因为→=→+→,→=→+→=→-2→,
所以→·→=(→+→)·(→-2→)=2→·→-2→2+→2=-2a2+4a+1.
由已知,得-2a2+4a+1=1.
又因为a>0,所以a=2,即AB的长为2.
12.已知P为△ABC所在平面内一点,且满足→=5→+5→,则△APB的面积与△APC的面积之比为________.
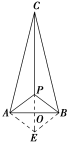 解析:由题意得,5→=→+2→,
解析:由题意得,5→=→+2→,
2→-2→=→-→-2→,
-2(→+→)=→,如图所示,以PA,PB为邻边作▱PAEB,
则C,P,E三点共线,连接PE交AB于点O,则→=2→=4→,
所以S△APC=S△APC=|PC|=2.
答案:1∶2
13.如图,已知在Rt△OAB中,∠AOB=90°,OA=3,OB=2,点M在OB上,且OM=1,点N在OA上,且ON=1,P为AM与BN的交点,则∠MPN=______.
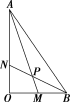
解析:设→=a,→=b,→与→的夹角为θ,
则→=2b,→=3a,
又因为→=→-→=2b-a,
→=→-→=3a-b.
所以→·→=b-a·a-b=-5,
又|→|=,|→|=,所以cos θ=10=-2.
又因为θ∈[0,π],所以θ=4,
又因为∠MPN为向量→,→的夹角,所以∠MPN=4.
答案:4
14.已知正方形ABCD,E,F分别是CD,AD的中点,BE,CF交于点P.求证:
(1)BE⊥CF;
(2)AP=AB.
证明:(1)以A为坐标原点,以→的方向为x轴的正方向,以→的方向为y轴的正方向,建立平面直角坐标系(图略),不妨设AB=2,
则A(0,0),B(2,0),C(2,2),D(0,2),E(1,2),F(0,1).
因为→=(-1,2),→=(-2,-1),
所以→·→=(-1)×(-2)+2×(-1)=0,
所以→⊥→,即BE⊥CF.
(2)设P(x,y),则→=(x,y-1),→=(-2,-1),
因为→∥→,所以-x=-2(y-1),即x=2y-2.①
同理,由→∥→,得y=-2x+4.②
由①②得x=5,y=5,即P5.
所以|→|2=5+5=4=|→|2,
所以|→|=|→|,即AP=AB.
[C 拓展探究]
15.一条宽为 km的河,水流速度为2 km/h,在河两岸有两个码头A,B,已知AB= km,船在水中最大航速为4 km/h,问该船从A码头到B码头怎样安排航行速度可使它最快到达彼岸B码头?用时多少?
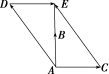 解:如图所示,设→为水流速度,→为航行速度,以AC和AD为邻边作▱ACED且当AE与AB重合时能最快到达彼岸,
解:如图所示,设→为水流速度,→为航行速度,以AC和AD为邻边作▱ACED且当AE与AB重合时能最快到达彼岸,
根据题意AC⊥AE,在Rt△ADE和▱ACED中,|→|=|→|=2,|→|=4,∠AED=90°,
所以|→|=|2=2.
又AB=,所以用时0.5 h.
因为sin∠EAD=2,∠EAD∈(0°,90°),
所以∠EAD=30°.
综上所述,船实际航行速度大小为2 km/h,与水流成120°角时能最快到达B码头,用时0.5 h.