5.5.2　简单的三角恒等变换

(教师独具内容)

课程标准：1.能用二倍角公式导出半角公式.2.了解三角恒等变换的特点、变换技巧，掌握三角恒等变换的基本思想方法.3.能利用三角恒等变换对三角函数式进行化简、求值以及证明三角恒等式．

教学重点：利用三角恒等变换对三角函数式化简、求值和证明．

教学难点：利用三角恒等变换来解决问题.

【知识导学】

知识点一　　　半角公式

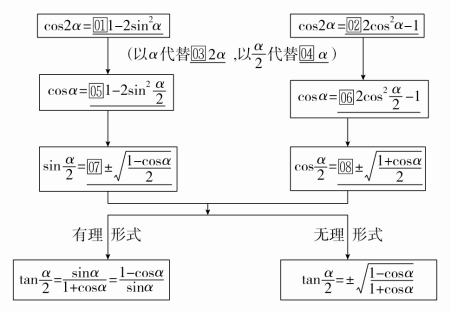
知识点二　　　积化和差与和差化积公式

(1)积化和差公式

sinαcosβ＝2(1)[sin(α＋β)＋sin(α－β)]．

cosαsinβ＝2(1)[sin(α＋β)－sin(α－β)]．

cosαcosβ＝2(1)[cos(α＋β)＋cos(α－β)]．

sinαsinβ＝－2(1)[cos(α＋β)－cos(α－β)]．

(2)和差化积公式

sinα＋sinβ＝2sin2(α＋β)cos2(α－β).

sinα－sinβ＝2cos2(α＋β)sin2(α－β).

cosα＋cosβ＝2cos2(α＋β)cos2(α－β).

cosα－cosβ＝－2sin2(α＋β)sin2(α－β).

【新知拓展】

辅助角公式

辅助角公式：asinx＋bcosx

＝sin(x＋φ)a(b).

推导过程：asinx＋bcosx

＝cosx(b).

令cosφ＝a2＋b2(a)，sinφ＝a2＋b2(b)，

则asinx＋bcosx＝(sinxcosφ＋cosxsinφ)＝sin(x＋φ)，

其中角φ所在象限由a，b的符号确定，角φ的值由tanφ＝a(b)确定或由sinφ＝a2＋b2(b)和cosφ＝a2＋b2(a)共同确定．

1．判一判(正确的打“√”，错误的打“×”)

(1)已知cosα＝3(1)，α∈(0，π)，则sin2(α)＝－3(3).(　　)

(2)cos²8(π)－4(1)＝4(2＋1).(　　)

(3)函数f(x)＝sinx＋cosx(x∈R)的最小正周期为π.(　　)

答案　(1)×　(2)√　(3)×

2．做一做

(1)若cosα＝3(1)，α∈(0，π)，则cos2(α)的值为(　　)

A.3(6)  B．－3(6)  C．±3(6)  D．±3(3)

(2)已知cosα＝5(4)，α∈，2π(3π)，则sin2(α)等于(　　)

A．－10(10)  B.10(10)  C.10(3)  D．－5(3)

(3)函数f(x)＝sin²x＋sinxcosx在区间2(π)上的最大值是(　　)

A．1  B.2(3)  C.2(3)  D．1＋

(4)若tanα＝2，则tan2(α)＝________.

答案　(1)A　(2)B　(3)C　(4)2(5)

题型一  利用半角公式求值

例1　已知sinα＝－5(4)，π<α<2(3π)，求sin2(α)，cos2(α)，tan2(α)的值．

[解]　∵π<α<2(3π)，sinα＝－5(4)，

∴cosα＝－5(3)，且2(π)<2(α)<4(3π)，

∴sin2(α)＝2(1－cosα)＝5(5)，

cos2(α)＝－2(1＋cosα)＝－5(5)，

tan2(α)＝2(α)＝－2.

金版点睛

由三角函数值求其他三角函数式的值的步骤

(1)若没有给出角的范围，则根号前的正负号需要根据条件讨论．一般讨论角所在象限．

(2)由三角函数值求其他三角函数式的值的步骤：

①先化简所求的式子．

②观察已知条件与所求式子之间的联系(从角和三角函数名称入手)．

③将已知条件代入所求式子，化简求值．

　已知sin2(α)－cos2(α)＝－5(1)，450°<α<540°，求tan2(α)的值．

解　由题意，得2(α)²＝5(1)，

即1－sinα＝5(1)，得sinα＝5(4).

∵450°<α<540°，∴cosα＝－5(3)，

∴tan2(α)＝sinα(1－cosα)＝5(4)＝2.

题型二  三角函数式的化简

例2　化简：()2()(π<α<2π)．

[解]　原式＝

2(α)

＝2(α)

＝()2(α).

又∵π<α<2π，∴2(π)<2(α)<π，∴cos2(α)<0，

∴原式＝()2(α)＝cosα.

[变式探究]　将本例改为化简：

()2()(180°<α<360°)．

解　原式＝

2(α)

＝2(α)

＝()2(α)＝()2(α).

∵180°<α<360°，∴90°<2(α)<180°，∴sin2(α)>0，

∴原式＝－cosα.

金版点睛

化简问题中的“三变”

(1)变角：三角变换时通常先寻找式子中各角之间的联系，通过拆、凑等手段消除角之间的差异，合理选择联系它们的公式．

(2)变名：观察三角函数种类的差异，尽量统一函数的名称，如统一为弦或统一为切．

(3)变式：观察式子的结构形式的差异，选择适当的变形途径．如升幂、降幂、配方、开方等．

　化简：

(1)－<θ<2π(3π)；

(2)2(α).

解　(1)原式＝2(θ)－2(θ)，

∵2(3π)<θ<2π，∴4(3π)<2(θ)<π，

∴0<sin2(θ)<2(2)，－1<cos2(θ)<－2(2)，

从而sin2(θ)＋cos2(θ)<0，sin2(θ)－cos2(θ)>0.

∴原式＝－2(θ)－2(θ)

＝－2sin2(θ).

(2)原式＝2(α)＝2(1)cos²α·2(α)

＝2(1)cos²α·tanα＝2(1)cosαsinα＝4(1)sin2α.

题型三  三角恒等式的证明

例3　求证：tan2(3x)－tan2(x)＝cosx＋cos2x(2sinx).

[证明]　证法一：tan2(3x)－tan2(x)＝2(3x)－2(x)

＝2(x)＝2(x)

＝2(x)＝2(x)

＝cosx＋cos2x(2sinx).

∴原式成立．

证法二：cosx＋cos2x(2sinx)＝2(x)

＝2(x)＝2(3x)－2(x)

＝tan2(3x)－tan2(x).

∴原式成立．

金版点睛

在三角恒等式的证明中，化繁为简是化简三角函数式的一般原则，按照目标确定化简思路，由复杂的一边化到简单的一边.如果两边都比较复杂，也可以采用左右归一的方法.

　求证：()()sin2αcos2β(sinα＋βsinα－β)＝1－tan2α(tan2β).

证明　证法一：左边＝

()()sin2αcos2β(sinαcosβ＋cosαsinβsinαcosβ－cosαsinβ)

＝sin2αcos2β(sin2αcos2β－cos2αsin2β)

＝1－sin2αcos2β(cos2αsin2β)＝1－tan2α(tan2β)＝右边．

∴原等式成立．

证法二：右边＝1－sin2αcos2β(cos2αsin2β)

＝sin2αcos2β(sin2αcos2β－cos2αsin2β)

＝()()sin2αcos2β(sinαcosβ＋cosαsinβsinαcosβ－cosαsinβ)

＝()()sin2αcos2β(sinα＋βsinα－β)＝左边．

∴原式成立.

题型四  利用辅助角公式研究函数性质

例4　已知函数f(x)＝sin6(π)＋2sin²12(π)(x∈R)．

(1)求函数f(x)的最小正周期；

(2)求使函数f(x)取得最大值的x的集合．

[解]　(1)∵f(x)＝sin6(π)＋2sin²12(π)

＝sin12(π)＋1－cos12(π)

＝212(π)＋1

＝2sin6(π)＋1

＝2sin3(π)＋1，

∴f(x)的最小正周期为T＝2(2π)＝π.

(2)当f(x)取得最大值时，sin3(π)＝1，

有2x－3(π)＝2kπ＋2(π)，即x＝kπ＋12(5π)(k∈Z)，

∴所求x的集合为{x，k∈Z(5π).

金版点睛

(1)为了研究函数的性质，往往要充分利用三角变换公式转化为正弦型(余弦型)函数，这是解决问题的前提.

(2)解此类题时要充分运用两角和(差)公式、二倍角公式、辅助角公式消除差异，减少角的种类和函数式的项数，为讨论函数性质提供保障.

　已知函数f(x)＝4cosxsin6(π)－1.

(1)求f(x)的最小正周期；

(2)求f(x)在区间4(π)上的最大值和最小值．

解　(1)f(x)＝4cosxsin6(π)－1

＝4cosxcosx(1)－1

＝sin2x＋2cos²x－1

＝sin2x＋cos2x

＝2sin6(π)，

所以f(x)的最小正周期为π.

(2)因为－6(π)≤x≤4(π)，所以－6(π)≤2x＋6(π)≤3(2π).

于是当2x＋6(π)＝2(π)，即x＝6(π)时，f(x)_max＝2；

当2x＋6(π)＝－6(π)，即x＝－6(π)时，f(x)_min＝－1.

题型五  三角变换的实际应用

例5　如图，A，B是半径为1的圆O上任意两点，以AB为一边作等边三角形ABC.当点A，B处于怎样的位置时，四边形OACB的面积最大？最大面积是多少？

[解]　如图，设∠AOB＝θ(0<θ<π)，四边形OACB的面积为S.取AB的中点D，连接OD，CD，则OD⊥AB，CD⊥AB.

在Rt△ODA中，OA＝1，∠AOD＝2(θ)，

所以AD＝OAsin∠AOD＝sin2(θ)，

OD＝OAcos∠AOD＝cos2(θ)，

所以AB＝2AD＝2sin2(θ).

因为△ABC为等边三角形，

所以CD＝ACsin∠CAB＝2sin2(θ)sin60°＝sin2(θ).

所以S＝S_△ABC＋S_△AOB

＝2(1)CD·AB＋2(1)OD·AB

＝2(1)×sin2(θ)×2sin2(θ)＋2(1)×cos2(θ)×2sin2(θ)

＝sin²2(θ)＋2(1)sinθ

＝×2(1－cosθ)＋2(1)sinθ

＝2(1)sinθ－2(3)cosθ＋2(3)

＝sin3(π)＋2(3).

因为0<θ<π，所以－3(π)<θ－3(π)<3(2π).

所以当θ－3(π)＝2(π)，即θ＝6(5π)时，S取得最大值1＋2(3).

所以当OA与OB的夹角为6(5π)时，四边形OACB的面积最大，最大面积是1＋2(3).

金版点睛

解答此类问题，关键是合理引入辅助角，先将实际问题转化为三角函数问题，再利用三角函数的有关知识求解.在求解过程中，要注意角的取值范围.

　有一块以O为圆心的半圆形空地，要在这块空地上划出一个内接矩形ABCD建为绿地，使其一边AD落在半圆的直径上，另外两点B，C落在半圆的圆周上．已知半圆的半径长为a，如何选择关于点O对称的点A，D的位置，才能使矩形ABCD的面积最大？

解　画出图形如图所示．

设∠AOB＝θ，θ∈2(π)，

则AB＝asinθ，OA＝acosθ.

设矩形ABCD的面积为S，

则S＝2OA·AB

＝2acosθ·asinθ＝a²·2sinθcosθ＝a²sin2θ.

因为θ∈2(π)，所以2θ∈(0，π)．

当2θ＝2(π)，即θ＝4(π)时，S_max＝a²，

此时点A，D距离点O均为2(2)a.

1．已知sinα＝5(3)2(π)，则cos2(α)等于(　　)

A.5(4)  B．－5(4)  C．－10(10)  D.10(10)

答案　D

解析　∵sinα＝5(3)且0<α<2(π)，∴cosα＝5(4).又cosα＝2cos²2(α)－1，∴cos²2(α)＝2(1＋cosα)＝10(9)，

∵0<2(α)<4(π)，∴cos2(α)＝10(10).

2.sin2α(2sin2α)·cos2α(2cos2α)等于(　　)

A．tanα  B．tan2α  C．1  D.2(1)

答案　B

解析　原式＝()sin2αcos2α(2sinαcosα2)＝sin2αcos2α(sin22α)＝cos2α(sin2α)＝tan2α.

3．函数y＝3sinx＋cosx，x∈2(π)的值域为________．

答案　[－3,2]

解析　函数y＝3sinx＋cosx＝2sin6(π)，

又x∈2(π)，

∴x＋6(π)∈3(2π)，

∴sin6(π)∈，1(3)，

∴2sin6(π)∈[－3,2]．

4．求值：2()＝________.

答案　－1

解析　2()＝2()

＝sin20°(1)＝－1.

5．已知函数f(x)＝sin3(π)＋sin3(π)＋2cos²x－1，x∈R.

(1)求函数f(x)的最小正周期；

(2)求函数f(x)在区间4(π)上的最大值和最小值．

解　(1)f(x)＝sin2xcos3(π)＋cos2xsin3(π)＋sin2xcos3(π)－cos2xsin3(π)＋cos2x＝sin2x＋cos2x＝sin4(π)，所以f(x)的最小正周期T＝2(2π)＝π.

(2)因为f(x)在区间8(π)上单调递增，在区间4(π)上单调递减，又f4(π)＝－1，f8(π)＝，f4(π)＝1，故函数f(x)在区间4(π)上的最大值为，最小值为－1.