![]()

![]() 5.4.1 正弦函数、余弦函数的图象
5.4.1 正弦函数、余弦函数的图象
![]() (教师独具内容)
(教师独具内容)
课程标准:1.了解利用单位圆画正弦曲线的方法.2.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.3.理解正弦曲线与余弦曲线之间的联系.
教学重点:正弦函数、余弦函数图象的作法.
教学难点:1.利用单位圆画正弦曲线.2.正弦曲线与余弦曲线之间的联系.
![]()
【知识导学】
知识点一 正弦函数的图象
(1)正弦曲线
正弦函数y=sinx,x∈R的图象叫做01正弦曲线.
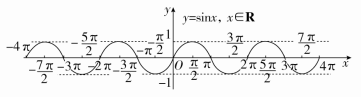
(2)正弦函数图象的画法
①几何法
(ⅰ)利用02单位圆画出y=sinx,x∈[0,2π]的图象;
(ⅱ)将图象不断03向左、向右平移(每次移动2π个单位长度).
②五点法
(ⅰ)画出正弦曲线在[0,2π]上的图象的五个关键点04(0,0),,1,(π,0),,-1,(2π,0),用光滑的曲线连接;
(ⅱ)将所得图象05向左、向右平行移动(每次移动2π个单位长度).
知识点二 余弦函数的图象
(1)余弦曲线
余弦函数y=cosx,x∈R的图象叫做01余弦曲线.
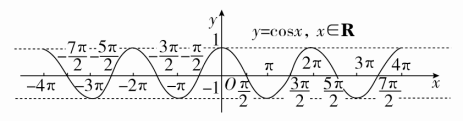
(2)余弦函数图象的画法
①要得到y=cosx的图象,只需把y=sinx的图象向左平移022个单位长度即可,这是由于cosx=sin2.
②用“五点法”画余弦曲线y=cosx在[0,2π]上的图象时,所取的五个关键点分别为03(0,1),,0,(π,-1),,0,(2π,1),再用光滑的曲线连接.将所得图象不断04向左、向右平移(每次移动2π个单位长度).
【新知拓展】
正弦曲线和余弦曲线是向左右两边无限延伸的,正弦曲线与余弦曲线形状相同,但在同一坐标系下的位置不同.
![]()
1.判一判(正确的打“√”,错误的打“×”)
(1)y=sinx,x∈[0,2π]的图象关于点P(π,0)成中心对称.( )
(2)y=cosx,x∈[0,2π]的图象关于直线x=2成轴对称.( )
(3)正弦函数、余弦函数的图象不超过直线y=1和y=-1所夹的范围.( )
(4)正弦曲线与余弦曲线形状相同,只是位置不同.( )
答案 (1)√ (2)× (3)√ (4)√
2.做一做
(1)下列各点中,不在y=sinx图象上的是( )
A.(0,0) B.,1
C.,-1 D.(π,1)
(2)从函数y=sinx,x∈[0,2π]的图象来看,对应于sinx=2的x有( )
A.1个值 B.2个值
C.3个值 D.4个值
(3)对于余弦函数y=cosx的图象,有以下描述:
①将[0,2π]内的图象向左向右无限伸展;
②与y=sinx的图象形状完全一样,只是位置不同;
③与y轴有无数个交点;
④关于y轴对称.
其中正确的描述有( )
A.1项 B.2项
C.3项 D.4项
答案 (1)D (2)B (3)C
![]()
题型一 五点法作图
例1 用“五点法”作出下列函数的简图:
(1)y=sinx-1,x∈[0,2π];
(2)y=2+cosx,x∈[0,2π].
[解] (1)列表:
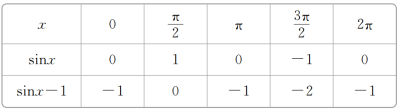
描点、连线,如图:

(2)列表:
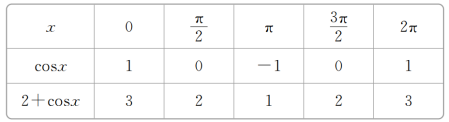
描点、连线,如图:

金版点睛
描点法画正弦函数图象(y=sinx)的关键
(1)列表时,自变量x的数值要适当选取
①在函数定义域内取值;②由小到大的顺序取值;③取的个数应分布均匀;④应注意图形中的特殊点(如:端点,交点,顶点);⑤尽量取特殊角.
(2)描点连线时应注意
①两坐标轴上的单位长度尽可能一致,以免改变图象的真实形状;
②变量x,y数值相差悬殊时,也允许采用不同长度单位;
③连线时一定要用光滑的曲线连接,防止画成折线.
作出下列函数的图象:
(1)y=-sinx(0≤x≤2π);
(2)y=1+cosx(0≤x≤2π).
解 (1)列表:
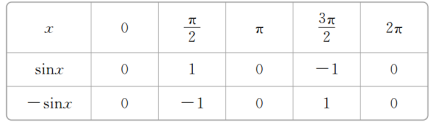
描点连线,如下图:
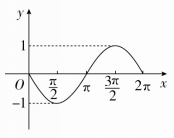
(2)列表:

描点连线,如下图:
题型二 用图象变换作函数图象
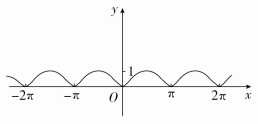
例2 作出函数y=的图象.
[解] y==|sinx|,
即y=()()-sinx2kπ+π<x<2kπ+2π(k∈Z).
其图象如下图:
金版点睛
用图象变换作函数图象
对于某些函数的图象,如y=-sinx,y=|sinx|,y=sin|x|等可通过图象变换,如平移变换、对称变换等作图.
(1)把y=sinx图象在x轴上方的保留,x轴下方的图象沿x轴翻折到x轴上方,就可得y=|sinx|的图象.
(2)把y=sinx图象在y轴右侧的保留,去掉y轴左侧的图象,再把y轴右侧的图象沿y轴翻折到y轴左侧,就可得y=sin|x|的图象.
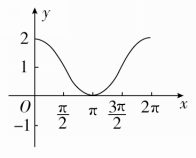
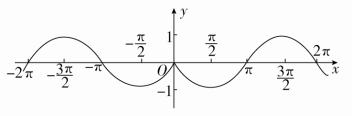
作出函数y=-sin|x|的图象.
解 y=-sin|x|=()()sinxx<0.
其图象如图所示:
题型三 正弦函数、余弦函数图象的简单应用
例3 利用正弦函数和余弦函数的图象,求满足下列条件的x的集合.
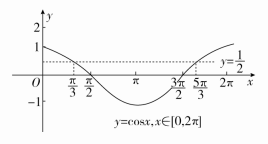
(1)sinx≥2;(2)cosx≤2.
[解] (1)作出正弦函数y=sinx,x∈[0,2π]的图象,如图所示,由图象可以得到满足条件的x的集合为+2kπ,k∈Z.

(2)作出余弦函数y=cosx,x∈[0,2π]的图象,如图所示,由图象可以得到满足条件的x的集合为+2kπ,k∈Z.
金版点睛
用三角函数图象解不等式的步骤
正弦函数、余弦函数图象的主要作用是解简单的三角不等式,用三角函数图象解不等式的步骤是:
(1)作出相应的正弦函数或余弦函数在[0,2π]上的图象;
(2)写出所求不等式在区间[0,2π]上的解集;
(3)根据诱导公式一写出定义域内的解集.
利用正弦曲线,求满足2<sinx≤2的x的集合.
解 首先作出y=sinx在[0,2π]上的图象.如图所示,
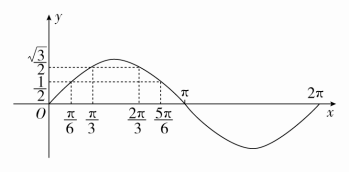
作直线y=2,根据特殊角的正弦值,可知该直线与y=sinx,x∈[0,2π]的交点横坐标为6和6;作直线y=2,该直线与y=sinx,x∈[0,2π]的交点横坐标为3和3.观察图象可知,在[0,2π]上,当6<x≤3或3≤x<6时,不等式2<sinx≤2成立,
所以2<sinx≤2的解集为{x|6+2kπ<x≤3+2kπ或3+2kπ≤x<6+2kπ,k∈Z}.
![]()
1.用“五点法”作y=sin2x的图象时,首先描出的五个点的横坐标是( )
A.0,2,π,2,2π B.0,4,2,4,π
C.0,π,2π,3π,4π D.0,6,3,2,3
答案 B
解析 根据“五点法”,可令2x=0,2,π,2,2π,解得x=0,4,2,4,π,故选B.
2.以下对正弦函数y=sinx的图象描述不正确的是( )
A.在x∈[2kπ,2kπ+2π](k∈Z)上的图象形状相同,只是位置不同
B.介于直线y=1与直线y=-1之间
C.关于x轴对称
D.与y轴仅有一个交点
答案 C
解析 由正弦函数图象可知,A正确;由正弦函数的图象可知B正确;由正弦函数的图象,知正弦函数的图象不关于x轴对称,关于原点对称,故C错误;由正弦函数图象,知D正确.故选C.
3.要得到正弦曲线,只要将余弦曲线( )
A.向右平移2个单位长度
B.向左平移2个单位长度
C.向右平移2个单位长度
D.向左平移π个单位长度
答案 A
解析 由于cos2=sinx,所以只需将y=cosx的图象向右平移2个单位长度即可.
4.满足cosx>0,x∈[0,2π]的x的取值范围是________.
答案 2∪,2π
解析 画出函数y=cosx,x∈[0,2π]的图象如图所示.
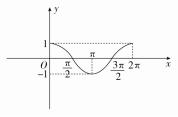
由图象可知满足cosx>0,x∈[0,2π]的x的取值范围为2∪,2π.
5.用“五点法”作出函数y=1+2sinx,x∈[0,2π]的图象.
解 列表:
x | 0 | 2 | π | 2 | 2π |
sinx | 0 | 1 | 0 | -1 | 0 |
1+2sinx | 1 | 3 | 1 | -1 | 1 |
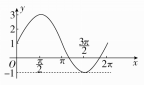
在直角坐标系中描出五点(0,1),,3,(π,1),,-1,(2π,1),然后用光滑曲线顺次连接起来,就得到y=1+2sinx,x∈[0,2π]的图象.