第2课时　诱导公式五、六

(教师独具内容)

课程标准：1.了解诱导公式五、六的意义和作用.2.理解诱导公式五、六的推导过程.3.能综合运用诱导公式一～六解决简单三角函数式的求值、化简与证明问题．

教学重点：诱导公式五、六的推导过程及诱导公式一～六的综合应用．

教学难点：诱导公式五、六的推导过程.

【知识导学】

知识点　诱导公式五、六

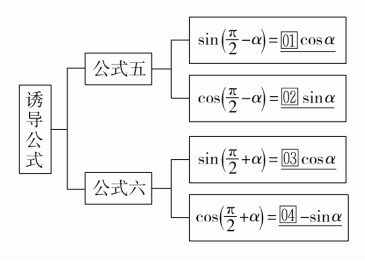
【新知拓展】

(1)公式五、六中的角α是任意角．

(2)诱导公式一～六中的角可归纳为k·2(π)±α的形式，可概括为“奇变偶不变，符号看象限”．

①“变”与“不变”是针对互余关系的函数而言的．

②“奇”“偶”是对诱导公式k·2(π)±α中的整数k来讲的．

③“象限”指k·2(π)±α中，将α看成锐角时，k·2(π)±α所在的象限，根据“一全正，二正弦，三正切，四余弦”的符号规律确定原函数值的符号．

(3)利用诱导公式五、六，结合诱导公式二，还可以推出如下公式：

sin－α(3π)＝－cosα，cos－α(3π)＝－sinα，

sin＋α(3π)＝－cosα，cos＋α(3π)＝sinα.

1．判一判(正确的打“√”，错误的打“×”)

(1)角2(π)－α与角α的终边关于y轴对称．(　　)

(2)由诱导公式五、六，能够推导出tan＋α(π)与tanα的关系．(　　)

(3)sin＋α(3π)＝－sinα.(　　)

答案　(1)×　(2)√　(3)×

2．做一做

(1)已知sin＋α(5π)＝5(1)，那么cosα＝(　　)

A．－5(2)    B．－5(1)  

C.5(1)   D.5(2)

(2)已知角α的终边经过点P₀(－3，－4)，则cos－α(π)的值为(　　)

A．－5(4)   B.5(3)  

C.5(4)    D．－5(3)

(3)化简：sin＋α(3π)＝________.

答案　(1)C　(2)A　(3)－cosα

题型一   利用诱导公式五、六求值

例1　已知cos＋α(π)＝3(1)，求值：

()－α()＋()()＋α().

[解]　原式＝－cosα(cosαsinα)＋－sinα(sinαsinα)

＝－sinα－sinα

＝－2sinα.

又cos＋α(π)＝3(1)，所以－sinα＝3(1).

所以原式＝－2sinα＝3(2).

金版点睛

诱导公式应用中需注意的问题

诱导公式的应用，就是化归思想的应用，求值过程就是由未知角的三角函数向已知角的三角函数的转化过程．解题时要密切注意角之间的关系，特别是互余、互补关系，为应用诱导公式创造条件．

　已知cos(π＋α)＝－2(1)，求cos＋α(π)的值．

解　∵cos(π＋α)＝－cosα＝－2(1)，

∴cosα＝2(1)，∴α为第一或第四象限角．

①若α为第一象限角，

则cos＋α(π)＝－sinα＝－

＝－2(1)＝－2(3)；

②若α为第四象限角，则

cos＋α(π)＝－sinα＝

＝2(1)＝2(3).

综上，cos＋α(π)＝2(3)或－2(3).

题型二  化简三角函数式

例2　化简：()－α()＋

()()＋α().

[解]　∵sin＋α(π)＝cosα，cos－α(π)＝sinα，

cos(π＋α)＝－cosα，sin(π－α)＝sinα，

cos＋α(π)＝－sinα，sin(π＋α)＝－sinα，

∴原式＝－cosα(cosαsinα)＋()－sinα(sinα·－sinα)

＝－sinα＋sinα＝0.

金版点睛

用诱导公式化简求值的方法

(1)对于三角函数式的化简求值问题，一般遵循诱导公式先行的原则，即先用诱导公式化简变形，达到角的统一，再进行三角函数名称转化，以保证三角函数名称最少．

(2)对于kπ±α(k∈Z)和2(π)±α这两套诱导公式，切记运用前一套公式不变名，而后一套公式必须变名．

　(1)sin²1°＋sin²2°＋sin²3°＋…＋sin²88°＋sin²89°＋sin²90°的值等于________；

(2)化简：()()－α(3π)＋()()cos2π＋α(3π).

答案　(1)2(91)　(2)见解析

解析　(1)因为sin²1°＋sin²89°＝sin²1°＋cos²1°＝1，

sin²2°＋sin²88°＝sin²2°＋cos²2°＝1，

sin²x°＋sin²(90°－x°)＝sin²x°＋cos²x°＝1(1≤x≤44，x∈N)，

所以原式＝(sin²1°＋sin²89°)＋(sin²2°＋sin²88°)＋…＋(sin²44°＋sin²46°)＋sin²90°＋sin²45°＝45＋2(2)²＝2(91).

(2)因为tan(3π－α)＝－tanα，sin(π－α)＝sinα，

sin－α(3π)＝－cosα，sin(2π－α)＝－sinα，

cos2(7π)＝cos2(π)＝－sinα，

sin＋α(3π)＝－cosα，cos(2π＋α)＝cosα，

所以原式＝()sinα－cosα(－tanα)＋()－cosαcosα(－sinα－sinα)

＝cos2α(1)－cos2α(sin2α)

＝cos2α(1－sin2α)＝cos2α(cos2α)＝1.

题型三  利用诱导公式证明三角恒等式

例3　求证：

()()()＋α(π)＝1.

[证明]　∵左边＝

()()()＋α(π)

＝()()()()－tanα－cosαsinα(－tanα－sinαcosα)＝1＝右边．

∴原式成立．

金版点睛

三角恒等式的证明策略

对于恒等式的证明，应遵循化繁为简的原则，从左边推到右边或从右边推到左边，也可以用左右归一、变更论证的方法．常用定义法、化弦法、拆项拆角法、“1”的代换法、公式变形法，要熟练掌握基本公式，善于从中选择巧妙简捷的方法．

　求证：()－1(3π)＋

()()＋θ(3π)＝sin2θ(2).

证明　∵左边＝()cosθ－cosθ－1(－cosθ)＋－cosθcosθ＋cosθ(cosθ)

＝1＋cosθ(1)＋1－cosθ(1)＝()()1＋cosθ1－cosθ(1－cosθ＋1＋cosθ)

＝1－cos2θ(2)＝sin2θ(2)＝右边．

∴原式成立．

1．已知sin40°＝a，则cos50°等于(　　)

A．±a    B．－a  

C．a   D.

答案　C

解析　cos50°＝cos(90°－40°)＝sin40°＝a.

2．已知sin2(π)＝3(1)，α∈，0(π)，则tanα的值为(　　)

A．－2    B．2  

C．－4(2)   D.4(2)

答案　A

解析　因为sin2(π)＝cosα＝3(1).

又α∈，0(π)，所以sinα＝－＝－3(2)，

则tanα＝－2.

3．已知tan(3π＋α)＝2，则

()()()()＋α()＝________.

答案　2

解析　由tan(3π＋α)＝2，得tanα＝2，所以

原式＝()()sinα－cosα(－sinα＋－cosα＋cosα－2－sinα)

＝sinα－cosα(sinα)＝tanα－1(tanα)＝2－1(2)＝2.

4．若sin＋θ(π)＝5(3)，则cos²θ－sin²θ＝________.

答案　－25(7)

解析　sin＋θ(π)＝cosθ＝5(3)，从而sin²θ＝1－cos²θ＝25(16)，所以cos²θ－sin²θ＝－25(7).

5．已知sin－α(π)＝2(1)，求cos＋α(π)sin＋α(2π)的值．

解　cos＋α(π)sin＋α(2π)

＝cos－α(π)sin－α(π)

＝sin－α(π)sin－α(π)＝2(1)×2(1)＝4(1).