第1课时　诱导公式二、三、四

(教师独具内容)

课程标准：1.了解三角函数的诱导公式的意义和作用.2.理解诱导公式的推导过程.3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题．

教学重点：诱导公式的推导过程及其应用．

教学难点：诱导公式的推导过程.

【知识导学】

知识点一  角的对称

(1)角π＋α的终边与角α的终边关于01(□)原点对称，如图a；

(2)角－α的终边与角α的终边关于02(□)x轴对称，如图b；

(3)角π－α的终边与角α的终边关于03(□)y轴对称，如图c.

知识点二  诱导公式

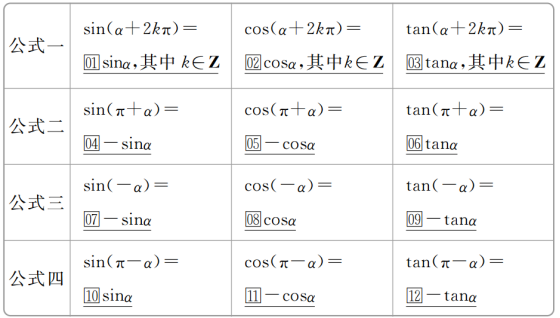
【新知拓展】

(1)在公式一～四中，角α是任意角．

(2)公式一、二、三、四都叫做诱导公式，它们可概括如下：

①记忆方法：2kπ＋α(k∈Z)，－α，π±α的三角函数值，等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号，可以简单地说成“函数名不变，符号看象限”．

②解释：“函数名不变”是指等式两边的三角函数同名；“符号”是指等号右边是正号还是负号；“看象限”是指假设α是锐角，要看原三角函数是取正值还是负值，如sin(π＋α)，若把α看成锐角，则π＋α在第三象限，正弦在第三象限取负值，故sin(π＋α)＝－sinα.

(3)利用诱导公式一和三，还可以得出如下公式：

sin(2π－α)＝－sinα，

cos(2π－α)＝cosα，

tan(2π－α)＝－tanα.

1．判一判(正确的打“√”，错误的打“×”)

(1)利用诱导公式二可以把第三象限角的三角函数化为第一象限角的三角函数．(　　)

(2)利用诱导公式三可以把负角的三角函数化为正角的三角函数．(　　)

(3)利用诱导公式四可以把第二象限角的三角函数化为第一象限角的三角函数．(　　)

(4)诱导公式二～四两边的函数名称一致．(　　)

(5)诱导公式中的角α只能是锐角．(　　)

答案　(1)√　(2)√　(3)√　(4)√　(5)×

2．做一做

(1)已知tanα＝4，则tan(π－α)等于(　　)

A．π－4    B．4  

C．－4    D．4－π

(2)sin6(7π)的值是(　　)

A．－2(1)    B．－2  

C．2  D.2(1)

(3)cos(3π＋α)＋cos(2π＋α)＝________.

答案　(1)C　(2)A　(3)0

题型一  给角求值问题

例1　求下列三角函数值：

(1)sin(－1200°)；(2)tan945°；(3)cos6(119π).

[解]　(1)sin(－1200°)＝－sin1200°

＝－sin(3×360°＋120°)＝－sin120°

＝－sin(180°－60°)

＝－sin60°＝－2(3).

(2)tan945°＝tan(2×360°＋225°)

＝tan225°＝tan(180°＋45°)

＝tan45°＝1.

(3)cos6(119π)＝cos6(π)

＝cos6(π)＝cos6(π)＝2(3).

金版点睛

利用诱导公式解决给角求值问题的步骤

　求下列各式的值：

(1)sin(－1320°)cos1110°＋cos(－1020°)sin750°＋tan495°；

(2)sin3(8π)cos6(31π)＋tan4(23π).

解　(1)原式＝sin(120°－4×360°)cos(30°＋3×360°)＋cos(60°－3×360°)sin(30°＋2×360°)＋tan(135°＋360°)＝sin120°cos30°＋cos60°sin30°＋tan135°＝2(3)×2(3)＋2(1)×2(1)－1＝0.

(2)原式＝sin3(2π)cos6(7π)＋tan4(π)

＝sin3(2π)cos6(7π)＋tan4(π)

＝sin3(π)·6(π)＋tan4(π)

＝2(3)×2(3)＋1＝4(1).

题型二  给值求值问题

例2　(1)已知cos(π－α)＝－5(3)，且α是第一象限角，则sin(－2π－α)的值是(　　)

A.5(4)    B．－5(4)  

C．±5(4)  D.5(3)

(2)已知cos－α(π)＝3(3)，则cos6(5π)＝________.

[解析]　(1)因为cos(π－α)＝－cosα，

所以cosα＝5(3).

因为α是第一象限角，所以sinα>0.

所以sinα＝＝2(3)＝5(4).

所以sin(－2π－α)＝sin(－α)＝－sinα＝－5(4).

(2)cos6(5π)＝cos－α(π)

＝－cos－α(π)＝－3(3).

[答案]　(1)B　(2)－3(3)

[结论探究]　(1)若本例(2)中的条件不变，求cos6(13π)；

(2)若本例(2)条件不变，求cos＋α(5π)－sin²6(π)的值．

解　(1)cos6(13π)＝cos－α(13π)＝cos－α(π)＝cos－α(π)＝3(3).

(2)因为cos＋α(5π)＝cos－α(π)

＝－cos－α(π)＝－3(3)，

sin²6(π)＝sin²－α(π)＝sin²－α(π)

＝1－cos²－α(π)＝1－3(3)²＝3(2)，

所以cos＋α(5π)－sin²6(π)＝－3(3)－3(2)

＝－3(3).

金版点睛

解决条件求值问题的策略

(1)解决条件求值问题，首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系．

(2)可以将已知式进行变形向所求式转化，或将所求式进行变形向已知式转化．

　(1)已知sinβ＝3(1)，cos(α＋β)＝－1，则sin(α＋2β)的值为(　　)

A．1    B．－1

C.3(1)    D．－3(1)

(2)已知cos(α－55°)＝－3(1)，且α为第四象限角，则sin(α＋125°)的值为________；

(3)已知tan(π＋α)＝3，求()()()()4cos－α＋sin2π－α(2cosπ－α－3sinπ＋α)的值．

答案　(1)D　(2)3(2)　(3)见解析

解析　(1)∵cos(α＋β)＝－1，∴α＋β＝π＋2kπ，k∈Z，

∴sin(α＋2β)＝sin[(α＋β)＋β]＝sin(π＋β)＝－sinβ＝－3(1).

(2)∵cos(α－55°)＝－3(1)<0，且α是第四象限角．

∴α－55°是第三象限角．

∴sin(α－55°)＝－()＝－3(2).

∵α＋125°＝180°＋(α－55°)，

∴sin(α＋125°)＝sin[180°＋(α－55°)]

＝－sin(α－55°)＝3(2).

(3)因为tan(π＋α)＝3，所以tanα＝3.

故()()()()4cos－α＋sin2π－α(2cosπ－α－3sinπ＋α)＝4cosα－sinα(－2cosα＋3sinα)

＝4－tanα(－2＋3tanα)＝4－3(－2＋3×3)＝7.

题型三   三角函数式的化简

例3　化简下列各式：

(1)()()()()()cosα－πsin5π－α(tan2π－αsin－2π－αcos6π－α)；

(2)sin250°＋cos790°(1＋2sin290°cos430°)；

(3)sin3(2π)cos3(4π)(k∈Z)．

[解]　(1)原式＝()()()()()()cosπ－αsinπ－α(·sin－αcos－α)

＝()()－cosαsinα(－sinα－sinα)＝－cosα(sinα)＝－tanα.

(2)原式＝()()()()sin180°＋70°＋cos720°＋70°(1＋2sin360°－70°cos360°＋70°)

＝－sin70°＋cos70°(1－2sin70°cos70°)＝cos70°－sin70°(|cos70°－sin70°|)

＝cos70°－sin70°(sin70°－cos70°)＝－1.

(3)当k为偶数时，

原式＝sin3(2π)cos3(4π)＝sin3(π)cos3(π)

＝－sin3(π)cos3(π)＝－4(3).

当k为奇数时，原式＝sin3(2π)cos3(4π)

＝sin3(π)cos3(π)

＝sin3(π)cos3(π)＝4(3).

金版点睛

三角函数式化简的常用方法

(1)依据所给式子合理选用诱导公式将所给角的三角函数转化为另一个角的三角函数．

(2)切化弦：一般需将表达式中的切函数转化为弦函数．

(3)注意“1”的应用：1＝sin²α＋cos²α＝tan4(π).

(4)用诱导公式进行化简时，若遇到kπ±α的形式，需对k进行分类讨论，然后再运用诱导公式进行化简．

　化简：(1)()()()sinπ－α(cos－αtan7π＋α)；

(2)()()()()cos－180°－αsin－α－180°(sin1440°＋αcosα－1080°).

解　(1)()()()sinπ－α(cos－αtan7π＋α)

＝()sinα(cosαtanπ＋α)＝sinα(cosαtanα)＝sinα(sinα)＝1.

(2)原式＝()()()()cos180°＋α·[－sin180°＋α](sin4×360°＋αcos3×360°－α)

＝()()－cosαsinα(sinαcos－α)＝－cosα(cosα)＝－1.

1．若n为整数，则化简()()cosnπ＋α(sinnπ＋α)所得的结果是(　　)

A．tannα    B．－tannα

C．tanα    D．－tanα

答案　C

解析　原式＝tan(nπ＋α)，无论n是奇数还是偶数，tan(nπ＋α)都等于tanα.

2．已知tan－α(π)＝3(1)，则tan＋α(2π)＝(　　)

A.3(1)    B．－3(1)

C.3(3)    D．－3(3)

答案　B

解析　因为tan＋α(2π)＝tan－α(π)＝－tan－α(π)，所以tan＋α(2π)＝－3(1).

3.()()sin495°＋sin－570°(cos－585°)的值等于________．

答案　－2

解析　原式＝()()()sin360°＋135°－sin210°＋360°(cos360°＋225°)

＝sin135°－sin210°(cos225°)

＝()()()sin180°－45°－sin180°＋30°(cos180°＋45°)

＝sin45°＋sin30°(－cos45°)＝2(1)＝－2.

4．已知sin(45°＋α)＝13(5)，则sin(225°＋α)＝________.

答案　－13(5)

解析　sin(225°＋α)＝sin[(45°＋α)＋180°]

＝－sin(45°＋α)＝－13(5).

5．化简：()()()()sinα＋nπcosα－nπ(sinα＋nπ＋sinα－nπ)(n∈Z)．

解　当n＝2k，k∈Z时，

原式＝()()()()sinα＋2kπcosα－2kπ(sinα＋2kπ＋sinα－2kπ)＝cosα(2).

当n＝2k＋1，k∈Z时，

原式＝()()()()sin[α＋2k＋1π]cos[α－2k＋1π](sin[α＋2k＋1π]＋sin[α－2k＋1π])

＝－cosα(2).

所以原式＝()()n为奇数.(2)