4.4.2　对数函数的图象和性质

第1课时　对数函数的图象和性质

(教师独具内容)

课程标准：能用描点法或借助计算工具画出具体对数函数的图象，探索并了解对数函数的单调性与特殊点．

教学重点：对数函数的图象及性质．

教学难点：底数a对图象的影响及对数函数性质的应用.

【知识导学】

知识点一　　　对数函数的图象和性质

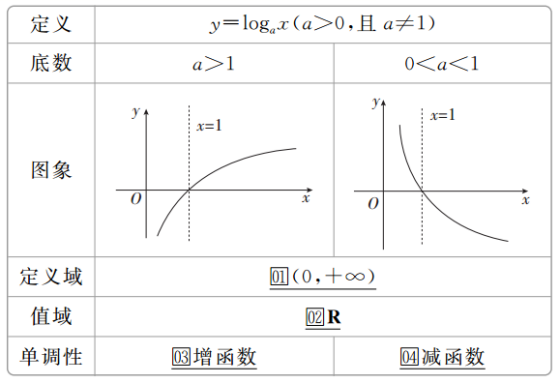
知识点二　　　指数函数与对数函数的关系

【新知拓展】

底数对函数图象的影响

对数函数y＝log₂x，y＝log₃x，y＝log12x，y＝log13x的图象如图所示，可得如下规律：

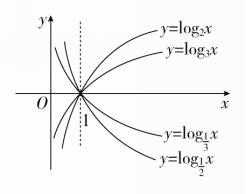
①y＝log_ax与y＝log1ax的图象关于x轴对称；

②当a＞1时，底数越大图象越靠近x轴；当0＜a＜1时，底数越小图象越靠近x轴．

1．判一判(正确的打“√”，错误的打“×”)

(1)对数函数的图象一定在y轴右侧．(　　)

(2)当0<a<1时，y＝log_ax在定义域上单调递增．(　　)

(3)函数y＝log_ax的定义域和值域均为(0，＋∞)．(　　)

答案　(1)√　(2)×　(3)×

2．做一做(请把正确的答案写在横线上)

(1)函数y＝log₃x(1≤x≤9)的值域为(　　)

A．[0，＋∞) B．R

C．(－∞，2] D．[0,2]

(2)若对数函数y＝log_(1－2a)x，x∈(0，＋∞)是增函数，则a的取值范围为________．

(3)已知y＝a^x在R上是增函数，则y＝log_ax在(0，＋∞)上是________函数．(填“增”或“减”)

答案　(1)D　(2)(－∞，0)　(3)增

题型一  对数函数的图象和性质

例1　如图所示的曲线是对数函数y＝log_ax，y＝log_bx，y＝log_cx，y＝log_dx的图象，则a，b，c，d,1,0的大小关系为________．

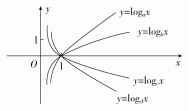
[解析]　由题图可知函数y＝log_ax，y＝log_bx的底数a>1，b>1，函数y＝log_cx，y＝log_dx的底数0<c<1,0<d<1.

过点(0,1)作平行于x轴的直线l(图略)，则直线l与四条曲线交点的横坐标从左向右依次为 c，d，a，b，显然b>a>1>d>c>0.

[答案]　b>a>1>d>c>0

金版点睛

根据对数函数的图象判断底数大小的方法

作直线y＝1与所给图象相交，交点的横坐标即为各个底数，依据在第一象限内，自左向右，图象对应的对数函数的底数逐渐变大，可比较底数的大小．

　已知0<a<1，函数y＝a^x与y＝log_a(－x)的图象可能是(　　)

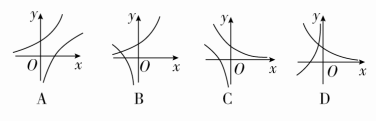
答案　D

解析　因为0<a<1，所以y＝a^x单调递减，y＝log_ax单调递减，而y＝log_a(－x)与y＝log_ax关于y轴对称，所以选D．

例2　若函数y＝log_a(x＋b)＋c(a>0，且a≠1)的图象恒过定点(3,2)，则实数b，c的值分别为_______．

[解析]　∵函数的图象恒过定点(3,2)，∴将(3,2)代入y＝log_a(x＋b)＋c，得2＝log_a(3＋b)＋C．又当a>0，且a≠1时，log_a1＝0恒成立，∴c＝2，由log_a(3＋b)＝0，得3＋b＝1，∴b＝－2.故填－2,2.

[答案]　－2,2

金版点睛

画对数函数图象时要注意的问题

(1)明确对数函数图象的分布区域．对数函数的图象在第一、四象限．当x趋近于0时，函数图象会越来越靠近y轴，但永远不会与y轴相交．

(2)建立分类讨论的思想．在画对数函数图象之前要先判断对数的底数a的取值范围是a>1，还是0<a<1.

(3)牢记特殊点．对数函数y＝log_ax(a>0，且a≠1)的图象经过点：(1,0)，(a,1)和，－1(1).

　函数y＝log_a(x＋1)－2(a>0，且a≠1)的图象恒过点________．

答案　(0，－2)

解析　因为函数y＝log_ax(a>0，且a≠1)的图象恒过点(1,0)，则令x＋1＝1，得x＝0，此时y＝log_a(x＋1)－2＝－2，所以函数y＝log_a(x＋1)－2(a>0，且a≠1)的图象恒过点(0，－2).

题型二  对数式的大小比较

例3　比较下列各组中两个值的大小：

(1)log₃1.9，log₃2；

(2)log₂3，log_0.32；

(3)log_aπ，log_a3.14(a>0，a≠1)．

[解]　(1)因为y＝log₃x在(0，＋∞)上是增函数，所以log₃1.9<log₃2.

(2)因为log₂3>log₂1＝0，log_0.32<log_0.31＝0，所以log₂3>log_0.32.

(3)当a>1时，函数y＝log_ax在(0，＋∞)上是增函数，则有log_aπ>log_a3.14；

当0<a<1时，函数y＝log_ax在(0，＋∞)上是减函数，则有log_aπ<log_a3.14.

综上所得，当a>1时，log_aπ>log_a3.14；当0<a<1时，log_aπ<log_a3.14.

金版点睛

比较对数式大小的常用方法

(1)比较同底的两个对数式的大小，常利用对数函数的单调性．

(2)比较不同底数的两个对数式的大小，常用以下两种方法：①先利用对数换底公式化为同底的对数，再利用对数函数的单调性比较大小；②在同一象限内利用对数函数图象的位置关系比较大小．

(3)比较底数与真数都不同的两个对数式的大小，常借助中间量(如1,0，－1等)．

(4)比较多个对数式的大小，则应先根据每个数的结构特征，以及它们与中间量“0”和“1”的大小情况进行分组，再比较各组内的对数式的大小即可．

(5)比较含参数的两个对数式的大小，要注意对底数是否大于1进行分类讨论，有时也要注意挖掘所给对数式的隐含条件．例如：比较log_a(b²－b＋1)与log_a2(1)的大小时，要注意隐含条件：b²－b＋1＝2(1)²＋4(3)≥4(3)>2(1).

　比较下列各组中两个值的大小：

(1)3log₄5,2log₂3；

(2)log₃0.2，log₄0.2；

(3)log₃π，log_π3；

(4)log_0.20.1,0.2^0.1.

解　(1)∵3log₄5＝log₄125,2log₂3＝log₂9＝log₄81，且函数y＝log₄x在(0，＋∞)上是增函数，又125>81，∴3log₄5>2log₂3.

(2)∵0>log_0.23>log_0.24，∴log0.23(1)<log0.24(1)，

即log₃0.2<log₄0.2.

(3)∵函数y＝log₃x在(0，＋∞)上是增函数，且π>3，∴log₃π>log₃3＝1.

同理，1＝log_ππ>log_π3，所以log₃π>log_π3.

(4)∵函数y＝log_0.2x在(0，＋∞)上是减函数，且0.1<0.2，∴log_0.20.1>log_0.20.2＝1.

∵函数y＝0.2^x在R上是减函数，且0<0.1，

∴0.2^0.1<0.2⁰＝1.

∴log_0.20.1>0.2^0.1.

题型三  与对数有关的函数的值域问题

例4　求下列函数的值域：

(1)y＝log₂(x²＋4)；(2)y＝log12 (3＋2x－x²)．

[解]　(1)y＝log₂(x²＋4)的定义域是R.

因为x²＋4≥4，所以log₂(x²＋4)≥log₂4＝2.

所以y＝log₂(x²＋4)的值域为[2，＋∞)．

(2)设u＝3＋2x－x²＝－(x－1)²＋4≤4.

因为u>0，所以0<u≤4.

又y＝log12u在(0,4]上为减函数，

所以log12u≥log124＝－2，

所以y＝log12 (3＋2x－x²)的值域为[－2，＋∞)．

金版点睛

(1)求与对数函数相关的复合函数的值域(最值)，关键是根据单调性求解，若需换元，需考虑新元的取值范围.

(2)对于形如y＝log_af(x)(a>0，且a≠1)的复合函数，其值域的求解步骤如下：

①分解成y＝log_au，u＝f(x)两个函数；

②求f(x)的定义域；

③求u的取值范围；

④利用y＝log_au的单调性求解.

　函数y＝lg (1＋32－x2)的值域为(　　)

A．(－∞，1) B．(0,1]

C．[0，＋∞) D．(1，＋∞)

答案　B

解析　∵2－x²≤2，∴0<32－x2≤9，∴1<1＋32－x2≤10，∴0<lg (1＋32－x2)≤1，∴y＝lg (1＋32－x2)的值域为(0,1].

题型四  与对数函数有关的函数图象问题

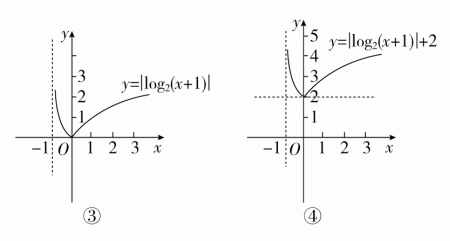
例5　作出函数y＝|log₂(x＋1)|＋2的图象．

[解]　第一步，作y＝log₂x的图象，如图①所示．

第二步，将y＝log₂x的图象沿x轴向左平移1个单位长度，得y＝log₂(x＋1)的图象，如图②所示．

第三步，将y＝log₂(x＋1)在x轴下方的图象作关于x轴的对称变换，得y＝|log₂(x＋1)|的图象，如图③所示．

第四步，将y＝|log₂(x＋1)|的图象沿y轴方向向上平移2个单位长度，便得到所求函数的图象，如图④所示．

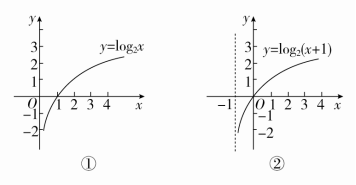
金版点睛

(1)一般地，函数y＝f(x±a)±b(a，b为正数)的图象可由函数y＝f(x)的图象变换得到.

将y＝f(x)的图象向左或向右平移a个单位长度可得到函数y＝f(x±a)的图象，再向上或向下平移b个单位长度可得到函数y＝f(x±a)±b的图象(记忆口诀：左加右减，上加下减).

(2)含有绝对值的函数的图象变换是一种对称变换，一般地，y＝f(|x－a|)的图象是关于x＝a对称的轴对称图形；函数y＝|f(x)|的图象是将y＝f(x)的图象在x轴上方的部分保留，将在x轴下方的部分作关于x轴的对称变换得到的.

(3)y＝f(x)的图象与y＝f(－x)的图象关于y轴对称，y＝f(x)的图象与y＝－f(x)的图象关于x轴对称.

　当x∈(1,2)时，不等式(x－1)²<log_ax恒成立，则a的取值范围是(　　)

A．(0,1) B．(1,2)

C．(1,2] D．2(1)

答案　C

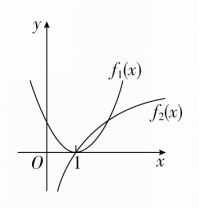
解析　设f₁(x)＝(x－1)²，f₂(x)＝log_ax，要使当x∈(1,2)时，不等式(x－1)²<log_ax恒成立，只需f₁(x)＝(x－1)²在(1,2)上的图象在f₂(x)＝log_ax的下方即可．当0<a<1时，显然不成立；当a>1时，如图所示，要使当x∈(1,2)时，f₁(x)＝(x－1)²的图象在f₂(x)＝log_ax的下方，只需f₁(2)≤f₂(2)，即(2－1)²≤log_a2，log_a2≥1，所以1<a≤2，故选C．

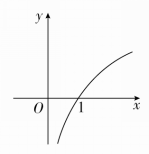
1．函数y＝log_ax的图象如图所示，则实数a的可能取值是(　　)

A．5   B．5(1)

C．e(1)   D．2(1)

答案　A

解析　∵函数y＝log_ax的图象逐渐上升，

∴函数y＝log_ax为单调增函数，∴a>1，故选A．

2．设a＝log₃2，b＝log₅2，c＝log₂3，则(　　)

A．a>c>b   B．b>c>a

C．c>b>a D．c>a>b

答案　D

解析　a＝log₃2<log₃3＝1；c＝log₂3>log₂2＝1，由对数函数的性质可知log₅2<log₃2，∴b<a<c，故选D．

3．函数f(x)＝log₃(x²＋1)的值域为(　　)

A．(0，＋∞) B．[0，＋∞)

C．(1，＋∞) D．[1，＋∞)

答案　B

解析　因为x²＋1≥1，且f(x)在[1，＋∞)上单调递增，所以log₃(x²＋1)≥log₃1＝0，故该函数的值域为[0，＋∞)．

4．若函数f(x)＝－5log_a(x－1)＋2(a>0，且a≠1)的图象恒过定点P，则点P的坐标是________．

答案　(2,2)

解析　令x－1＝1，得x＝2，即f(2)＝2，故P(2,2)．

5．若函数f(x)为定义在R上的奇函数，且x∈(0，＋∞)时，f(x)＝lg (x＋1)，求f(x)的表达式，并画出大致图象．

解　∵f(x)为R上的奇函数，∴f(0)＝0.

又当x∈(－∞，0)时，－x∈(0，＋∞)，

∴f(－x)＝lg (1－x)．

又f(－x)＝－f(x)，

∴f(x)＝－lg (1－x)，

∴f(x)的解析式为

f(x)＝()()－lg 1－x，x<0，(0，x＝0，)

f(x)的大致图象如图所示．