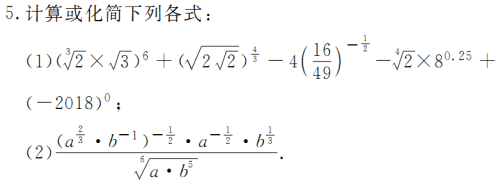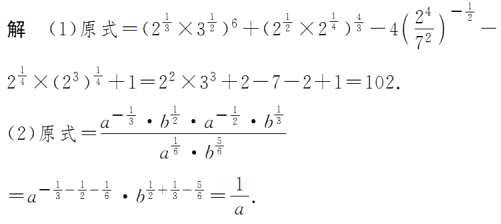4.1.2　无理数指数幂及其运算性质

(教师独具内容)

课程标准：1.了解指数幂由有理数扩充到无理数的过程.2.理解指数幂的运算性质.3.能进行指数幂(实数幂)的运算．

教学重点：1.指数幂由有理数扩充到无理数的过程.2.实数指数幂的运算．

教学难点：无理数指数幂的意义的理解．

【知识导学】

知识点一　无理数指数幂

(1)对于无理数指数幂，我们只需要了解两点：①它是一个确定的实数；②它是有理数指数幂无限逼近的结果．

(2)定义了无理数指数幂之后，幂的指数就由原来的有理数范围扩充到了实数范围．

知识点二　实数指数幂的运算性质

(1)a^ra^s＝01(□)a^r＋s(a>0，r，s∈R)．

(2)(a^r)^s＝02(□)a^rs(a>0，r，s∈R)．

(3)(ab)^r＝03(□)a^rb^r(a>0，b>0，r∈R)．

【新知拓展】

对于实数a＞0，r，s有a^r ÷a^s＝a^r－s成立．这是因为a^r÷a^s＝as(ar)＝a^r·a^－s＝a^r－s.教材中没有给出此性质，但是它可以由已有公式推导出来．

(1)在进行幂和根式的化简时，一般原则是：先将负指数幂化为正指数幂，将小数化为分数，将根式化为分数指数幂，将底数(较大的整数分解质因数)化成指数幂的形式，再利用幂的运算性质在系数、同底数幂间进行运算，达到化简和求值的目的．

(2)化简指数幂的几个常用技巧如下：

①a(b)^－p＝b(a)^p(ab≠0)；

②a＝(am(1)m(1))^m，am(n)m(n)＝(am(1)m(1))ⁿ(a使式子有意义)；

1.判一判(正确的打“√”，错误的打“×”)

(1)α，β是实数，当a>0时，(a^α)^β＝(a^β)^α.(　　)

(2)当a>0，b>0时，(a2(1)2(1)＋b2(1)2(1))(a2(1)2(1)－b2(1)2(1))＝a－b^－1.(　　)

(3)当a>0时，(a－a^－1)²＝(a＋a^－1)²－2.(　　)

(4)[()^－2] 2(1)2(1)＝.(　　)

(5)(3^－2) 2(1)2(1)×()^－2＝9(1).(　　)

答案　(1)√　(2)√　(3)×　(4)×　(5)√

2.做一做(请把正确的答案写在横线上)

(1)化简：(3^－)＝________.

(2)已知5^α＝3,5^β＝2，则

①5^α＋β＝________；

②5^α－β＝________；

③5^－3α＝________；

④52(α)2(α)＝________.

答案　(1)27(1)　(2)①6　②2(3)　③27(1)　④

题型一  利用指数幂的运算性质化简与求值

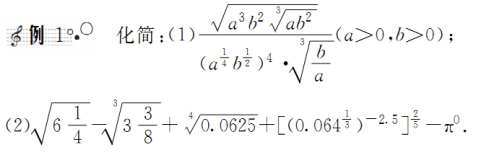
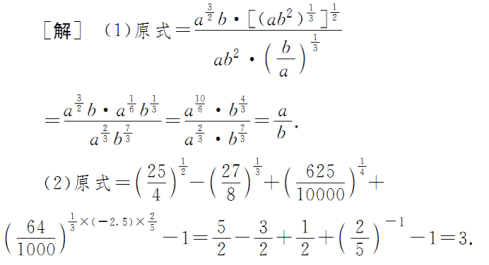
金版点睛

指数幂的一般运算步骤

有括号先算括号里的；无括号先做指数运算．负指数幂化为正指数幂的倒数．底数是负数，先确定符号，底数是小数，先要化成分数，底数是带分数，先要化成假分数，然后要尽可能用幂的形式表示，便于用指数幂的运算性质.

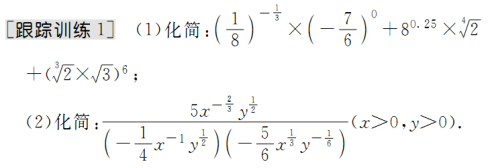
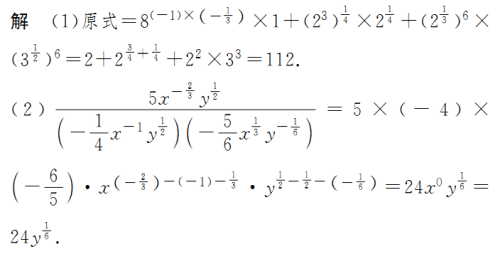
题型二  条件求值问题

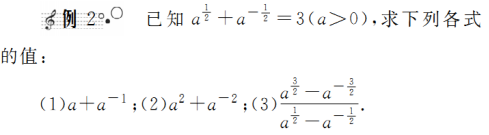
金版点睛

解决条件求值问题的一般方法——整体代入法

对于条件求值问题，一般先化简代数式，再将字母取值代入求值．但有时字母的取值不知道或不易求出，这时可将所求代数式恰当地变形，构造出与已知条件相同或相似的结构，从而通过“整体代入法”巧妙地求出代数式的值．

利用“整体代入法”求值常用的变形公式如下(其中a>0，b>0)：

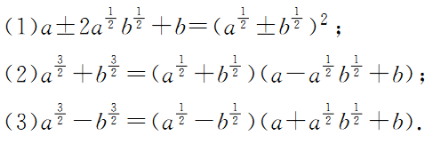
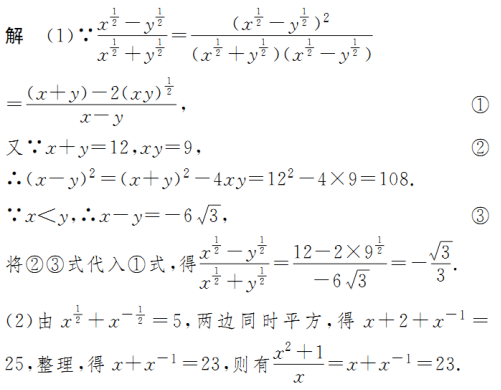
1.a(3)·－a(6)等于(　　)

A.－   B．－

C.   D.

答案　A

解析　a(3)·－a(6)＝a3(1)3(1)·(－a) 6(1)6(1)＝－(－a) 3(1)3(1)·(－a) 6(1)6(1)＝－(－a) 2(1)2(1)＝－.

2.81(16) 4(1)4(1)的值是(　　)

A.3(2)  B.2(3)  C.81(4)  D．－4(81)

答案　B

解析　81(16)4(1)4(1)＝4(2)4(1)4(1)＝3(2)^－1＝2(3).

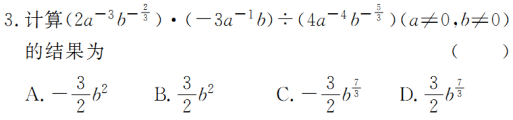
答案　A

解析　原式＝[2×(－3)÷4]×a^－3－1＋4·b3(2)3(5)3(5)＝－2(3)a⁰b²＝－2(3)b².

4.化简(＋)²⁰¹⁸·(－)²⁰¹⁹＝________.

答案　－

解析　(＋)²⁰¹⁸·(－)²⁰¹⁹＝[(＋)(－)]²⁰¹⁸·(－)＝1²⁰¹⁸·(－)＝－.