(教师独具内容)

课程标准：1.通过具体实例了解幂函数的概念.2.会画幂函数y＝x，y＝x²，y＝x³，y＝x(1)，y＝x2(1)2(1)的图象，并能通过图象了解幂函数的图象与性质.3.能正确应用幂函数的知识解决相关问题．

教学重点：1.幂函数的概念.2.幂函数的图象与性质．

教学难点：应用幂函数的知识解决相关问题．

【知识导学】

知识点一　幂函数的概念

一般地，函数01(□)y＝x^α叫做幂函数(power function)，其中02(□)x是自变量，03(□)α是常数．

知识点二　一些常用幂函数的图象

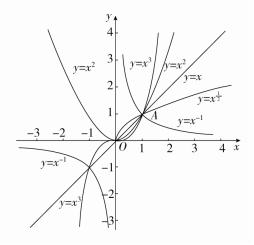
同一坐标系中，幂函数y＝x，y＝x²，y＝x³，y＝x^－1，y＝x2(1)2(1)的图象(如图)．

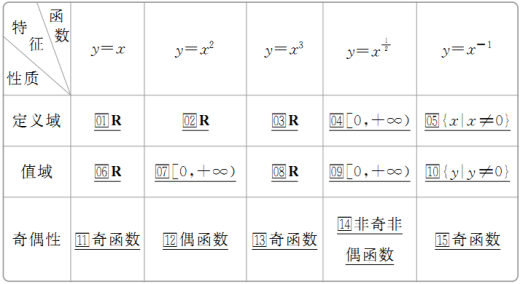
知识点三　一些常用幂函数的性质

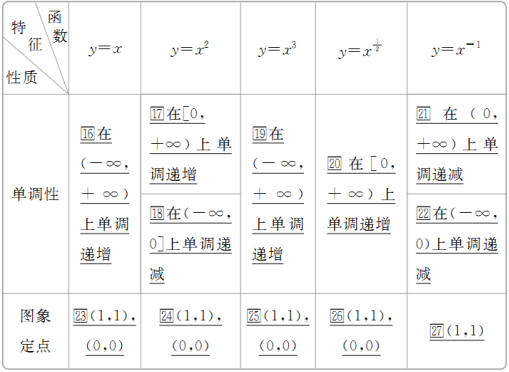
【新知拓展】

1．幂函数的特征

(1)x^α的系数是1；

(2)x^α的底数x是自变量；

(3)x^α的指数α为常数．

只有满足这三个条件，才是幂函数．对于形如y＝(2x)^α，y＝2x⁵，y＝x^α＋6等的函数都不是幂函数．

2．幂函数的性质

(1)所有的幂函数在(0，＋∞)上都有定义，并且图象都过点(1,1)；

(2)如果α＞0，那么幂函数的图象过原点，并且在区间[0，＋∞)上单调递增；

(3)如果α＜0，那么幂函数的图象在区间(0，＋∞)上单调递减，在第一象限内，当x从右边趋向于原点时，图象在y轴右方无限接近y轴，当x从原点趋向于＋∞时，图象在x轴上方无限接近x轴；

(4)在(1，＋∞)上，随幂指数的逐渐增大，图象越来越靠近y轴．

1．判一判(正确的打“√”，错误的打“×”)

(1)函数y＝x³＋2是幂函数．(　　)

(2)幂函数的图象必过(0,0)和(1,1)这两点．(　　)

(3)幂函数y＝x^α的定义域为R，与指数无关．(　　)

(4)当x＞1时，函数y＝x²的图象总在函数y＝x³的图象的下方．(　　)

答案　(1)×　(2)×　(3)×　(4)√

2．做一做(请把正确的答案写在横线上)

(1)若y＝mx^α＋(2n－4)是幂函数，则m＋n＝________.

(2)已知幂函数f(x)＝x^α的图象经过点(2,8)，则f(－2)＝________.

(3)若y＝ax2(1)2(1)是幂函数，则该函数的值域是________．

答案　(1)3　(2)－8　(3)[0，＋∞) 

题型一  幂函数的定义

例1　已知幂函数y＝(m²－m－1)x^m2－2m－3，求此幂函数的解析式，并指出其定义域．

[解]　∵y＝(m²－m－1)x^m2－2m－3为幂函数，

∴m²－m－1＝1，解得m＝2或m＝－1.

当m＝2时，m²－2m－3＝－3，则y＝x^－3，且有x≠0；

当m＝－1时，m²－2m－3＝0，则y＝x⁰，且有x≠0.

故所求幂函数的解析式为y＝x^－3或y＝x⁰，它们的定义域都是{x|x≠0}．

金版点睛

判断函数是幂函数的依据

判断一个函数是否为幂函数的依据是该函数是否为y＝x^α(α为常数)的形式，即满足：①指数α为常数；②底数x为自变量；③系数为1.

　(1)在函数y＝x2(1)，y＝2x²，y＝x²＋x，y＝1中，幂函数的个数为(　　)

A．0  B．1  C．2  D．3

(2)已知y＝(m²－4m＋4)xm－1(1)m－1(1)＋2n－3是幂函数，求m，n的值．

答案　(1)B　(2)见解析

解析　(1)y＝x2(1)＝x^－2，所以是幂函数；y＝2x²由于系数是2，因此不是幂函数；y＝x²＋x是两项和的形式，不是幂函数；y＝1＝x⁰(x≠0)，可以看出，常函数y＝1的图象比幂函数y＝x⁰的图象多了一个点(0,1)，所以常函数y＝1不是幂函数．

(2)由题意得2n－3＝0，(m－1≠0，)解得，(3)

所以m＝3，n＝2(3).

题型二  幂函数的图象及应用

例2　幂函数y＝x²，y＝x^－1，y＝x2(1)2(1)，y＝x2(1)2(1)在第一象限内的图象依次是图中的曲线(　　)

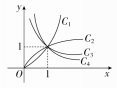
A．C₂，C₁，C₃，C₄

B．C₄，C₁，C₃，C₂

C．C₃，C₂，C₁，C₄

D．C₁，C₄，C₂，C₃

[解析]　由于在第一象限内直线x＝1的右侧，幂函数y＝x^α的图象从上到下相应的指数α由大变小，即幂函数图象在第一象限内直线x＝1右侧的“高低”关系是“指大图高”，故幂函数y＝x²在第一象限内的图象为C₁，y＝x^－1在第一象限内的图象为C₄，y＝x2(1)2(1)在第一象限内的图象为C₂，y＝x2(1)2(1)在第一象限内的图象为C₃.

[答案]　D

金版点睛

解决幂函数图象问题应把握的两个原则

(1)依据图象高低判断幂指数大小，相关结论为：在(0,1]上，指数越大，幂函数图象越靠近x轴(简记为指大图低)；在[1，＋∞)上，指数越大，幂函数图象越远离x轴(简记为指大图高)．

(2)依据图象确定幂指数α与0,1的大小关系，即根据幂函数在第一象限内的图象(类似于y＝x^－1或y＝x2(1)2(1)或y＝x³)来判断．

　(1)如图是幂函数y＝x^m与y＝xⁿ在第一象限内的图象，则(　　)

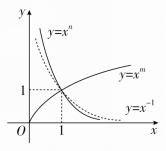
A．－1<n<0<m<1

B．n<－1,0<m<1

C．－1<n<0，m>1

D．n<－1，m>1

(2)已知函数y＝.

①求定义域；

②判断奇偶性；

③已知该函数在第一象限的图象如图所示，试补全图象，并由图象确定单调区间．

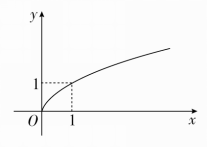
答案　(1)B　(2)见解析

解析　(1)在(0,1)内取x₀，作直线x＝x₀，与各图象有交点，则“点低指数大”．如图，0<m<1，n<－1.

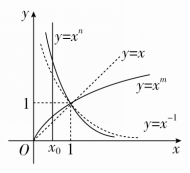
(2)①y＝，定义域为实数集R.

②设y＝f(x)，因为f(－x)＝＝＝f(x)，且定义域关于坐标原点对称，所以函数y＝是偶函数．

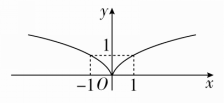
③因为函数为偶函数，则作出它在第一象限的图象关于y轴的对称图象，即得函数y＝的图象，如图所示．

根据图象易知，函数y＝在区间[0，＋∞)上单调递增，在区间(－∞，0]上单调递减.

题型三  幂函数的性质及应用

例3　比较下列各题中两个值的大小：

(1)2.32(1)2(1)，2.42(1)2(1)；

(2)() 2(1)2(1)，()2(1)2(1)；

(3)(－0.31)^2,0.35².

[解]　(1)∵y＝x2(1)2(1)在[0，＋∞)上单调递增，且2.3<2.4，∴2.32(1)2(1)<2.42(1)2(1).

(2)∵y＝x2(1)2(1)在(0，＋∞)上单调递减，且<，

∴()2(1)2(1)>()2(1)2(1).

(3)∵y＝x²为R上的偶函数，∴(－0.31)²＝0.31².

又函数y＝x²在[0，＋∞)上单调递增，且0.31<0.35，

∴0.31²<0.35²，即(－0.31)²<0.35².

金版点睛

比较幂值大小的方法

比较幂值的大小，关键是构造适当的函数，若指数相同，底数不同，则考虑构造幂函数，然后根据所构造的幂函数的性质如单调性、奇偶性等来解决问题．

例4　若(3－2m) 2(1)2(1)>(m＋1) 2(1)2(1)，求实数m的取值范围．

[解]　因为y＝x2(1)2(1)在定义域[0，＋∞)上单调递增，

所以3－2m>m＋1，(m＋1≥0，)解得－1≤m<3(2).

故实数m的取值范围为3(2).

金版点睛

利用幂函数解不等式的步骤

利用幂函数解不等式，实质是已知两个函数值的大小，判断自变量的大小，常与幂函数的单调性、奇偶性等综合命题．求解步骤如下：

(1)确定可以利用的幂函数；

(2)借助相应的幂函数的单调性，将不等式的大小关系，转化为自变量的大小关系；

(3)解不等式(组)求参数范围，注意分类讨论思想的应用．

　(1)比较下列各组数的大小：

①3(2)2(1)2(1)与5(3)2(1)2(1)；②－3.14³与－π³；

(2)已知幂函数y＝(m²＋m－5)x^m2－2m－3，当x∈(0，＋∞)时，y随x的增大而减小，求此幂函数的解析式．

解　(1)①∵y＝x2(1)2(1)在[0，＋∞)上单调递增，且3(2)>5(3)，

∴3(2)2(1)2(1)>5(3)2(1)2(1).

②∵y＝x³是R上的增函数，且3.14<π，

∴3.14³<π³，∴－3.14³>－π³.

(2)∵y＝(m²＋m－5)x^m2－2m－3是幂函数，

∴m²＋m－5＝1，即(m－2)(m＋3)＝0，

∴m＝2或m＝－3.

当m＝2时，m²－2m－3＝－3，y＝x^－3是幂函数，且满足当x∈(0，＋∞)时，y随x的增大而减小；

当m＝－3时，m²－2m－3＝12，y＝x¹²是幂函数，但不满足当x∈(0，＋∞)时，y随x的增大而减小，故舍去．

∴y＝x^－3(x≠0)．

1．下列函数是幂函数的是(　　)

A．y＝5^x   B．y＝x⁵

C．y＝5x   D．y＝(x＋1)³

答案　B

解析　由幂函数的定义知函数y＝5^x不是幂函数；函数y＝5x是正比例函数，不是幂函数；函数y＝(x＋1)³的底数不是自变量x，不是幂函数；函数y＝x⁵是幂函数．

2．函数y＝x³的图象大致是图中的(　　)

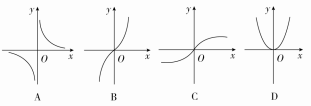
答案　B

解析　∵函数y＝x³是奇函数，且α＝3>1，则其为增函数，且y随x的增大急剧增大，∴函数图象为B.

3．设a＝2^－6，b＝3^－4，c＝7^－2，则a，b，c的大小关系为(　　)

A．b<a<c  B．a<c<b

C．a<b<c  D．c<b<a

答案　A

解析　a＝2^－6＝8^－2，b＝3^－4＝9^－2，c＝7^－2，由幂函数y＝x^－2在(0，＋∞)上单调递减，可知b<a<c.

4．已知幂函数f(x)的图象过点(4,2)，则f8(1)＝________.

答案　4(2)

解析　设幂函数为y＝x^α(α为常数)．

∵函数f(x)的图象过点(4,2)，∴2＝4^α，

∴α＝2(1)，∴f(x)＝x2(1)2(1)，

∴f8(1)＝8(1)2(1)2(1)＝4(2).

5．已知幂函数y＝x^3m－9(m∈N^*)的图象关于y轴对称，且在区间(0，＋∞)上单调递减，求f(x)的解析式．

解　∵幂函数y＝x^3m－9在区间(0，＋∞)上单调递减，

∴3m－9<0，即m<3.

又∵m∈N^*，∴m＝1,2.

又y＝x^3m－9的图象关于y轴对称，即该函数是偶函数，

∴3m－9是偶数．∴m＝1.

∴f(x)＝x^－6.