![]()

 (教师独具内容)
(教师独具内容)
课程标准:1.理解子集、真子集的概念,能识别给定集合的子集.2.理解两个集合包含与相等的含义,能用子集的观点解释两个集合的相等关系.
教学重点:1.子集、真子集定义的理解.2.写出给定集合的子集.3.两个集合之间关系的判定.4.用子集观点解释两个集合的相等关系.
教学难点:1.两个集合之间关系的判定.2.一些关系符号(⊆,⊇,,,∈,∉)的准确使用.3.具体问题中易忽视空集的情况.
![]()
【知识导学】
知识点 一 子集
一 子集
一般地,对于两个集合A,B,如果集合A中任意一个元素01都是集合B中的元素,就称集合A为集合B的02子集,记作A⊆B(或B⊇A),读作“A包含于B”(或“B包含A”).
注意:(1)子集是刻画两个集合之间关系的,它反映的是局部与整体之间的关系(而元素与集合之间的关系是个体与整体之间的关系).
(2)并不是任意两个集合之间都具有包含关系.例如:A={1,2},B={1,3},因为2∈A,但2∉B,所以A不是B的子集;同理,因为3∈B,但3∉A,所以B也不是A的子集.
(3)子集有下列两个性质:
①自反性:任何一个集合都是它本身的子集,即A⊆A;
②传递性:对于集合A,B,C,如果A⊆B,且B⊆C,那么A⊆C.
知识点 二 Venn图
二 Venn图
为了直观地表示集合间的关系,常用平面上封闭曲线的内部代表集合,这种图称为01Venn图.因此,A⊆B可用02Venn图表示为
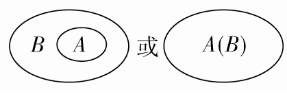
知识点 三 集合相等
三 集合相等
一般地,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素都是集合A的元素,那么集合A与集合B01相等,记作A=B.
也就是说,若A⊆B,且B⊆A,则A=B.
很明显,若两个集合相等,则它们的元素完全相同;若集合A与B中有不相同的元素,则这两个集合不相等,可记为A≠B.
知识点 四 真子集
四 真子集
如果集合A⊆B,但存在元素x∈B,且x∉A,就称集合A是集合B的01真子集(proper subset),记作02AB(或BA).
从真子集的定义可以看出,要想证明A是B的真子集,需要两步:一是证明03A⊆B(即A中的任何元素都属于B),二是证明04A≠B(即B中的元素不是都属于A,或者说B中至少有一个元素不属于A).
知识点 五 空集
五 空集
一般地,我们把不含任何元素的集合叫做01空集,记为02∅,并规定:03空集是任何集合的子集.
在这个规定的基础上,结合子集和真子集的有关概念,可以得到:
(1)空集04只有一个子集,即05它本身;
(2)空集是06任何非空集合的真子集.
【新知拓展】
1.对子集、真子集有关概念的理解
(1)集合A中的任何一个元素都是集合B中的元素,即由x∈A,能推出x∈B,这是判断A⊆B的常用方法.
(2)不能简单地把“A⊆B”理解成“A是B中部分元素组成的集合”.因为若A=∅时,则A中不含任何元素;若A=B,则A中含有B中的所有元素.
(3)在真子集的定义中,AB首先要满足A⊆B,其次至少有一个x∈B,但x∉A.
2.集合子集的个数
求集合的子集问题时,一般可以按照子集元素个数分类,再依次写出符合要求的子集.
集合的子集、真子集个数的规律为:含n个元素的集合有2n个子集,有(2n-1)个真子集,有(2n-2)个非空真子集.写集合的子集时,空集和集合本身易漏掉.
3.0,{0},∅,{∅}的关系
∅与0 | ∅与{0} | ∅与{∅} | |
相同点 | 都表示无 的意思 | 都是集合 | 都是集合 |
不同点 | ∅是集合; 0是实数 | ∅中不含任何元素;{0}含一个元素0 | ∅不含任何元素;{∅}含一个元素,该元素是∅ |
关系 | 0∉∅ | ∅{0} | ∅{∅}或 ∅∈{∅} |

1.判一判(正确的打“√”,错误的打“×”)
(1)若A⊆B,则B中至少有一个元素不属于A.( )
(2)若A⊆B,则要么AB,要么A=B.( )
(3)空集没有真子集.( )
(4)若A⊆B,则B不会是空集.( )
(5)若A=B,则必有A⊆B.( )
答案 (1)× (2)√ (3)√ (4)× (5)√
2.做一做(请把正确的答案写在横线上)
(1)用适当的符号(⊆,⊇,,,=)填空:
N*________N,R________Q,
{x|x2=1}________{-1,1},
{(x,y)|x+y=1}________()x-y=0.
(2)给出下列集合:A={x|x是平行四边形},B={x|x是矩形},C={x|x是菱形},D={x|x是正方形},它们的关系可以表示为________________.
答案 (1) = (2)DBA,DCA

题型一 判断集合之间的关系
例1 判断下列各组集合之间的关系:
(1)A={1,2,4},B={x|x是8的正约数};
(2)A={x|x是等边三角形},B={x|x是有一个内角是60°的等腰三角形};
(3)A={x|x=2n-1,n∈N*},B={x|x=2n+1,n∈N*}.
[解] (1)集合A中的元素1,2,4都是8的正约数,从而这三个元素都属于B,即A⊆B;但B中的元素8不属于A,从而A≠B,所以AB.
(2)等边三角形都是有一个内角是60°的等腰三角形,即A⊆B;有一个内角是60°的等腰三角形是等边三角形,即B⊆A,所以A=B.
(3)解法一:两个集合都表示一些正奇数组成的集合,但由于n∈N*,因此集合A含有元素“1”,而集合B不含元素“1”,故BA.
解法二:由列举法知A={1,3,5,7,…},B={3,5,7,9,…},所以BA.
金版点睛
集合之间的关系是由两集合中元素的关系确定的,因此,要判定集合之间的关系,必须根据集合的表示方法,弄清集合中的元素是什么,再根据元素之间的关系给出结果;很明显当AB或者A=B时,不宜表示为A⊆B.
例1中(3),两集合中条件“n∈N*”改为n∈Z,结果如何?
解 A=B.
题型二 写出集合的子集
例2 写出集合{a,b,c}的所有子集.
[解] 因为集合{a,b,c}中有3个元素,所以其子集中的元素个数只能是0,1,2,3.
有0个元素的子集:∅;
有1个元素的子集:{a},{b},{c};
有2个元素的子集:{a,b},{a,c},{b,c};
有3个元素的子集:{a,b,c}.
因此集合{a,b,c}的所有子集为∅,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}.
金版点睛
本例采用分类列举的方法,分类的标准是子集中元素的个数,这样做,所写的子集不重不漏,是一种思路清晰、条理明确的解题方法.
写出集合{1,2,3}的所有子集.
解 ∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}.
题型三 有限集子集个数探究
例3 令集合A0=∅,集合An={a1,a2,a3,…,an}(n∈N*),试探究集合An子集的个数.
[解] 为了方便,不妨设集合An的子集数为m(An).我们把An的子集分为两类,第一类:含元素an;第二类:不含元素an.易知,第二类就是集合An-1的子集,且第一类和第二类同样多.因此,m(An)=2m(An-1).从而,m(An-1)=2m(An-2),…,m(A1)=2m(A0),易知m(A0)=1.所以m(An)=2m(An-1)=22m(An-2)=23m(An-3)=…=2nm(A0)=2n.
金版点睛
若一组对象分为甲、乙两类,当两类对象同样多时,我们只要知道其中一类对象的个数,也就知道了另一类对象的个数,从而也就知道了这组对象的总个数.“同样多”是一种一一对应的观点.
如下例:

注意:如果非空集合A中有n(n∈N*)个元素,那么集合A的子集有2n个,真子集有(2n-1)个,非空真子集有(2n-2)个.
满足{1,2}M⊆{1,2,3,4,5}的集合M有多少个?
解 由{1,2}M可知,M中必定有1,2两个元素,且至少还有异于1,2的“其他”一个元素;由M⊆{1,2,3,4,5}可知,上面所说的“其他”应当来自于3,4,5这三个数:可以是其中的1个(三种情况),2个(三种情况),3个(一种情况).故满足条件的集合M有7个(也就是集合{3,4,5}的非空子集的个数).
题型四 含参问题探究
例4 已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.若BA,求实数m的取值范围.
[解] ①当B≠∅时,如图所示:
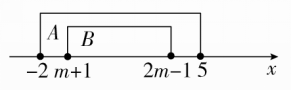
∴2m-1≥m+1或2m-1≥m+1,
解这两个不等式组,得2≤m≤3.
②当B=∅时,由m+1>2m-1,得m<2.综上可得,m的取值范围是{m|m≤3}.
金版点睛
本例的难点是解读集合B,事实上,集合B就是不等式组x≤2m-1
的解集(只是写法不同),易知当m+1>2m-1,即m<2时,不等式组无解,即B=∅;当m=2时,B={3};当m>2时,从几何角度讲,集合B是数轴上一条变端点、变长度的线段.
已知集合A={x|-3≤x≤4},B={x|2m-1<x<m+1},且B⊆A.求实数m的取值范围.
解 B⊆A,分两种情况考虑:
①当B=∅时,m+1≤2m-1,
解得m≥2.
②当B≠∅时,有2m-1<m+1,
解得-1≤m<2,
综上得实数m的取值范围为{m|m≥-1}.

1.下列说法:
①空集没有子集;②任何集合至少有两个子集;③空集是任何集合的真子集;④若∅A,则A≠∅.其中正确的有( )
A.0个 B.1个
C.2个 D.3个
答案 B
解析 ①空集是它本身的子集;②空集只有一个子集;③空集不是它本身的真子集;④空集是任何非空集合的真子集.因此,①②③错误,④正确.
2.集合P={0,1},Q={y|x2+y2=1,x∈N},则集合P,Q间的关系是( )
A.P=Q B.PQ
C.QP D.不确定
答案 B
解析 由x2+y2=1,x∈N,得y=±1,0,即Q={-1,0,1},所以PQ.故选B.
3.已知集合A={x|x2-1=0},则下列式子表示正确的有( )
①1∈A;②{-1}∈A;③∅⊆A;④{1,-1}⊆A.
A.1个 B.2个
C.3个 D.4个
答案 C
解析 A={x|x2-1=0}={-1,1},故①③④正确,②不正确.
4.满足{a}⊆M{a,b,c,d}的集合M共有( )
A.6个 B.7个
C.8个 D.15个
答案 B
解析 依题意a∈M,且M{a,b,c,d},因此M中必含有元素a,且可含有元素b,c,d中的0个、1个或2个,即M的个数等于集合{b,c,d}的真子集的个数,有23-1=7(个).
5.已知集合A={x|1≤x≤2},B={x|1≤x≤a,a≥1}.
(1)若A是B的真子集,求a的取值范围;
(2)若B是A的子集,求a的取值范围;
(3)若A=B,求a的取值范围.
解 (1)若AB,由图可知a>2.
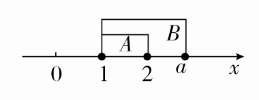
(2)若B⊆A,由图可知1≤a≤2.
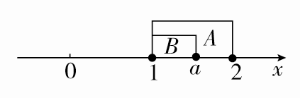
(3)由A=B,可得a=2.