A 卷
开始测试
B 卷
二、解答题
9、启明公司生产某种产品，每件产品成本3元，售价为4元，年销售量为10万件，为了获得更大利润，公司准备拿出一定资金做广告宣传，根据经验，每年投入的广告费是x（万元）时，产品的年销售量将是原销售量的y倍，且 如果把利润看作是销售总额减去成本费和广告费，试写出年利润S（万元）与广告费（万元）的函数关系式，并计算广告费是多少万元时，公司获得年利润最大，最大年利润是多少？
[答案]
10、某商场通过调查发现，某种玩具如果售价定为10元，日销量为50件，售价每提高1元，日销售量将减少3件。试问商场要获得最大日销售额，该玩具的销售价应该定为多少元，此时日销售额为多少？(价格取整数)
[答案]
11、某种炮弹的射程为1千米，飞行路线为抛物线。在某次战斗中，它曾经射中与它水平距离为750米，高度为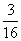 千米的目标。试问这种炮弹是否有可能击中高度为300米的目标？若能，请设计一种方案，若不能，请说明理由。
[答案]
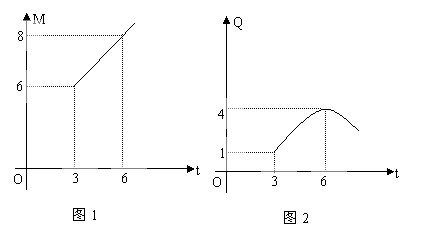
12、某商业公司指导某种应季商品的生产和销售，对三月份至七月份该商品的售价和生产进行了调研，结果如下：一件商品的售价M（元）与时间t(月)的关系可用一条线段上的点来表示（如图1）；一件商品的成本Q（元）与时间t（月）的关系可用一条抛物线上的点来表示，其中6月份成本最高（如图2）.
根据图象提供的信息解答下面问题：
（1）一件商品在3月份出售时的利润是多少元？
（2）求图2中表示的一件商品的成本Q（元）与时间t（月）之间的函数关系式；
（3）你能求出三月份至七月份一件商品的利润W（元）与时间t(月)之间的函数关系式吗？若该公司能在一个月内售出此种商品30000件，请你计算一下该公司在一个月内至少获利多少元？
[答案]
13、某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下图所示的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前七个月的利润总和s和t之间的关系)．根据图象提供的信息，解答下列问题：
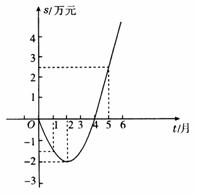
(1)由已知图象上的三点坐标，求累积利润s(万元)与时间t(月)之间的函数关系式；
(2)求截止到几月末公司累积利润可达到30万元?
(3)求第7个月公司所获利润是多少万元?
[答案]
14、某商场销售某种品牌的纯牛奶，已知进价为每箱40元，生产厂家要求每箱售价在40元～70元之间．市场调查发现，若每箱以50元销售，平均每天可销售90箱；价格每降低1元，平均每天多销售3箱；价格每升高1元，平均每天少销售3箱．
（1）写出平均每天销售量y（箱）与每箱售价x（元）之间的函数关系式．（注明范围）
（2）求出商场平均每天销售这种牛奶的利润W（元）与每箱牛奶的售价x（元）之间的二次函数关系式．（每箱的利润=售价－进价）
（3）求出（2）中二次函数图象的顶点坐标，并求当x=40，70时W的值，在给出的坐标系中画出函数图象的草图．
（4）由函数图象可以看出，当牛奶售价为多少时，平均每天的利润最大？最大利润为多少？
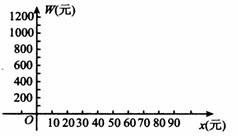
[答案]
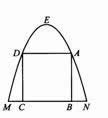
15、如图，有一块铁皮，拱形边缘呈抛物线状，MN=40cm，抛物线的顶点到边MN的距离为40cm.要在铁皮上截下一矩形ABCD，使矩形的顶点B、C落在边MN上，A、D在抛物线上，问这样截下的矩形铁皮的周长能否等于80cm？（提示：以MN所在直线为x轴，建立适当的平面直角坐标系）
[答案]
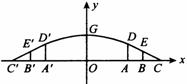
16、如图所示，这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图，横断面的地平线为x轴，横断面的对称轴为y轴，拱桥的DGD′部分为一段抛物线，顶点G的高度为8m，AD和A′D′是两侧高为5.5m的支柱，OA和OA′为两个方向的汽车通行区，宽都为15m，线段CD和C′D′为两段对称的上桥斜坡，其坡度为1︰4．
（1）求桥拱DGD′所在抛物线的关系式及CC′的长；
（2）BE和B′E′为支撑斜坡的支柱，其高都为4米，相应的AB和A′B′为两个方向的行人及非机动车通行区，求AB和A′B′的宽；
（3）按规定，汽车通过该桥下时，载货最高处和桥拱之间的距离不得小于0.4m．今有一大型运货汽车，装载某大型设备后，其宽为4m，车载大型设备的顶部分与地面的距离均为7m，它能否从OA（或OA′）区域安全通过？请说明理由．
[答案]
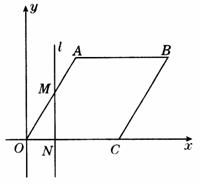
17、如图所示，在平面直角坐标系中，四边形OABC为菱形，点C的坐标为(4,0)，∠AOC=60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方)．
(1)求A、B两点的坐标；
(2)设△OMN的面积为S，直线l运动时间为t秒(0≤t≤6)，试求S与t的函数表达式；
(3)在题(2)的条件下，t为何值时，S的面积最大?最大面积是多少?
[答案]
|
