例：如图所示，⊙M与x轴交于A、B两点，其坐标分别为A（－3，0）、B（1，0），直径CD垂直于x轴于N，直线CE切⊙M于C，直线FG切⊙M于F，交CE于G，已知G点的横坐标为3．

　　（1）若抛物线y=－x2－2x＋m经过A、B、D三点，求m的值及点D的坐标；

　　（2）求直线DF的关系式；

　　（3）是否存在过点G的直线，使它与（1）中抛物线的两个交点的横坐标之和等于4？若存在，请求出满足条件的直线的关系式；若不存在，请说明理由．

分析：

　　（1）中抛物线经过A、B、D三点，可将A或B的坐标代入函数关系式，求出m值；因为圆是一个轴对称图形，CD为⊙M直径，所以D在抛物线对称轴上.

解：

　　（1）把A（－3，0）代入y=－x2－2x＋m，得0=－9＋6＋m，∴m=3．

　　∴抛物线为y=－x2－2x+3．点D在抛物线的对称轴上，所以D点横坐标为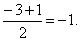

　　当x=－1时，y=－1+2+3=4，∴D（－1，4）.

　　（2）连结MG交y轴于H，设DF交y轴于Q.

　　∵GC与GF均是⊙M的切线，

　　∴△MCG≌△MFG，则∠FMG=∠CMG=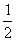∠FMC.

　　又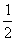∠FMC=∠MDF=∠MFD，∴∠MFD=∠FMG.

　　∴DF||MG（内错角相等，两直线平行）.

　　设M点坐标为（－1，y），则在Rt△MNB中有MN=y，NB=2，则MB=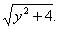

　　又MB=DM=4－y，得y=.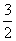

　　即有M点坐标为（－1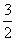，），C点坐标为（－1，－1），

　　则G点坐标为（3，－1）.直线MG为y=－.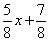

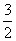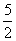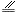　　又MD=4－=，且MDHQ，

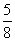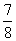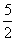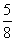　　∴直线DF的关系式为将直线MG的关系式向上平移MD个单位即有y=－x++=－x+.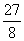

　　（3）假设存在过G点的直线为y=kx+b.把G（3，－1）代入，得3k+b=－1.

　　∴b=－1－3k.

　　

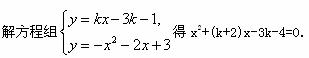
　　由题意，得－2－k=4.∴k=－6.

　　当k=－6时，=(k＋2)2－4(－3k－4)=16－56=－40﹤0.

　　∴方程无实根.

　　∴方程组无实数解，∴满足条件的直线不存在.

点拨：结合图形特点分析数量关系.

　　　　　　　　　　　　　　　　　　　　　　　　　-END-