1、有理化因式
(1)有理化因式的定义:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就称这两个代数式互为有理化因式.
(2)求有理化因式的方法
①如果含有二次根式的代数式是单项式,即开方如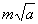 的式子,它的有理化因式就是
的式子,它的有理化因式就是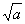 (
(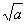 是最简二次根式).
是最简二次根式).
②如果含有二次根式的代数式是二项式,那么它的有理化因式也是二项式,其中有一项与原二项式中的一项完全相同,另一项与原二项式中的另一项只差一个符号,即它们相乘恰好满足平方差公式.
(3)一般常见的互为有理化因式有如下几种类型:①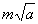 与
与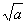 ;②
;②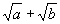 与
与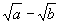 ;③
;③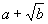 与
与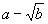 ;④
;④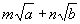 与
与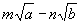 (其中
(其中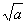 、
、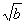 都是最简二次根式).
都是最简二次根式).
2、分母有理化
当被开方式中含有分母时,要把分母中的根号化去,这个运算过程叫分母有理化.如分母含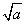 时,分子分母同乘以
时,分子分母同乘以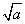 ;分母为
;分母为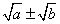 形式,分子分母同乘以
形式,分子分母同乘以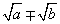 ,以便运用平方差公式,化去分母中的根号.
,以便运用平方差公式,化去分母中的根号.
例1、化简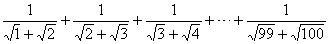
分析:
当分母里二次根式的被开方数都相差1时,如果分母有理化后则变为1或-1,就可将原式变为不含分母的二次根式.
解:
原式=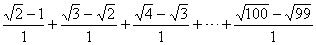
=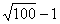
=10-1
=9
注意:这种解题方法是一种常用的技巧,应掌握.
例2、 化简:
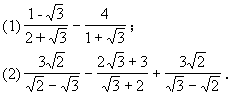
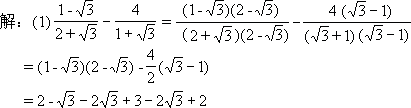
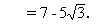
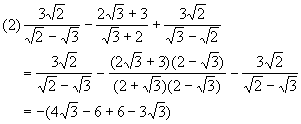
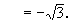
总结:
在计算过程中要注意各个式子的特点,能否约分或消项(第2小题)达到化简的目的,又要善于在规则允许的情况下可交换相邻项的位置,如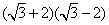 ,结果为-1,继续运算易出现符号上的差错,而把
,结果为-1,继续运算易出现符号上的差错,而把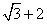 变为
变为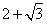 ,这样
,这样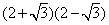 则为1,继续运算可避免错误.
则为1,继续运算可避免错误.